我从初中毕业的暑假开始学习离散数学，参考的是胡新启的那本书。
本文主要摘要了当时的学习笔记，包含的是第四章的代数系统和群论部分，以及第二、三章中涉及到的必要知识。

二元关系

等价关系、商集

对于非空集合 A 上的关系 R，如果它是自反、传递、对称的，那么 R 是 A 上的等价关系。
例如三角形的相似、集合中的相等都是等价关系。

设 R 是非空集合 A 上的等价关系，a ∈ A。定义等价类为 A 中和 a 具有关系 R 的全体元素组成的子集，记为 $[a]_R$。

$$
[a]_R = \{ x | x \in A , x R a \}
$$

A 的等价类的全体构成的集合，称为商集。容易看出，商集是集合的集合。
$$
A / R = \{ [a]_R | a \in A \}
$$

设 R 是非空集合 A 上的等价关系，则商集 A / R 是 A 的一个划分。反之，对于集合 A 的任意划分 π，可确定 A 上的一个等价关系 R，且 R 对应的商集 A / R = π。

相容关系

非空集合 A 上的关系 R，如果是自反的、对称的，称为 A 上的相容关系。

极大相容类。

偏序关系

函数

单射、满射、双射

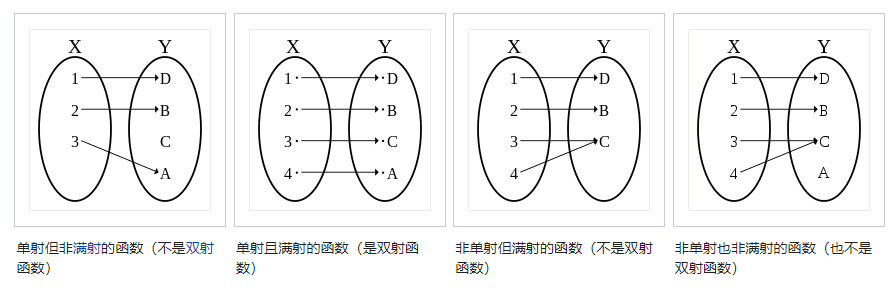
像和原(逆)像。

反函数

集合 A 上的恒等关系是 A 上的函数，称为 A 上的恒等函数 $ I_A $。
如果反函数存在，则

代数运算和代数系统

运算律

任何两个二元运算比如 $ 和 %，服从吸收律如果:

1	a $ (a % b) = a % (a $ b) = a.

运算 $ 和 % 被称为对偶对。
从直觉上来讲，好像 a 把 (a % b) 或者 (a $ b) 吸收了一样。集合的交并集运算满足吸收律，我们可以从文恩图上获得直觉。

幺元/单位元。
零元。
逆元。

唯一零元、单位元。

代数系统

代数系统。
对于代数系统V = (A, +, *)，如果 A0 包含于 A，且 A0 对于 + 和 * 都封闭，则V0 = (A0, +, *)也是代数系统，并称为 A 的子代数。

积代数。

同态和同构

考虑两个二元代数系统 U = (A, *, +) 和 V = (B, **, ++)，并且它们是同类型的。即 *和**都同是二元运算。**和++也一样。
如果存在从 A 到 B 的映射 h，使得对于任意的 a,b ∈ A 都有

1 2	h(a * b) = h(a) ** h(b) h(a + b) = h(a) ++ h(b)

那么 h 是从 U 到 V 的一个同态映射。h(A) 是 A 的一个同态像。如果 U 等于 V，则 h 是 A 上的自同态。

如果 h 是单射，则 h 是单同态；h 是满射，h 是满同态；h 是双射，h 同构映射，也称为 U 和 V 同构。

定义从 R+ 到 R 上的映射 f(x) = ln(x)，它是(R+, *)到(R, +)的一个同构映射。

设 $ U = (A, +, \times) $ 和 $ V = (B, \oplus, \otimes) $。都是二元运算。h 是从 U 到 V 的满同态。则：

如果$ \times $满足结合律，则 $ \otimes $满足结合律
…
如果 A 对 $ \times $有单位元 e，则 B 对 $ \otimes $有单位元 h(e)
如果 A 对 $ + $有零元 θ，则 B 对 $ \oplus $有零元 h(θ)

商代数

设代数系统 (A, *)，R 为 A 上的等价关系。如果满足下面的条件，则称为同余关系
$$
\forall a , b , a’ , b’ \in A , aRa’ , bRb’ , \rightarrow (a * b) R (a’ * b’)
$$

不妨举例，对于任意的 i,j ∈ Z，$ i \equiv_m j \iff m | (i - j) $。现在验证 $\equiv_m$ 是 (Z, +, *) 上的同余关系。

证明 $\equiv_m$ 是等价关系
【自反】即证明 $ \left \langle x,x \right \rangle \in \equiv_m $。显然 m 能整除 $x - x = 0$。
【对称】即证明 $ \forall x, y \in A , \left \langle x,y \right \rangle \in \equiv_m \Rightarrow \left \langle y,x \right \rangle \in \equiv_m $。这很简单，只是加个负号而已。
【传递】即证明 $ \forall x, y, z \in A , \left \langle x,y \right \rangle \in \equiv_m, \left \langle y,z \right \rangle \in \equiv_m \Rightarrow \left \langle x,z \right \rangle \in \equiv_m $。这个可以得到 x - z = (p + q)m
证明加法
实际就是要证明 $ \forall a , b , a’ , b’ \in Z $，如果 $ a \equiv_m a’ , b \equiv_m b’ $，则 $ (a + b) \equiv_m (a’ + b’) $。
简单展开下 $\equiv_m$ 就可以得到证明了。

给出代数系统 (A, *)，和这之上的同余关系 R，这里的 $ *_R $是一个新运算，满足 $[x]_R *_R [y]_R = [x * y]_R $。

于是，可以构造出一个新的代数系统 $ (A/R, *_R) $，称为 $(A, *)$ 关于 R 的商代数。

可以构造出 $(A, *)$ 到 $ (A/R, *_R) $ 的满同态 f：

$$
f : A \rightarrow A / R : f(a) = [a]_R, \forall a \in A
$$

这个同态称为自然同态。

刚才，同余关系 R 诱导出了从一个代数系统到它的商代数的一个同态 f。现在我们考虑是否可以从一个同态映射诱导出一个同余关系。
假设 h 是从 (A, +) 到 (B, *) 的同态映射，可以定义从 h 诱导的 A 的关系 $R_h$ 为如下，此时 $R_h$ 是 A 上的同余关系

$$
a R_h b \iff h(a) = h(b), \forall a, b \in A
$$

代数学同态基本定理

设 h 是从 $ (A, +) $ 到 $ (B, *) $ 的一个满同态，$ R_h $ 是 h 诱导的 $ (A, +) $ 上的同余关系，则 R 下的商代数 $ (A / R_h, +_h) $ 和 $ (B, *) $ 同构。

不妨设

$$
f: A / R_h \rightarrow B: f([a]_{R_h}) = h(a)
$$

我们就是要证明：
令
$$
x = [a]_{R_h} \ , y = [b]_{R_h},
$$
则
$$
\forall x, y \in A / R_h, f(x +_h y) = f(x) * f(y)
$$

容易得到如下。实际上是根据商代数的定义，以及同态的定义来推导的。

$$
f([a]_{R_h} +_h [b]_{R_h}) =
f([a + b]_R) =
h(a + b) =
h(a) * h(b) =
f([a]_{R_h}) * f([b]_{R_h})
$$

下面证明 f 是双射：

f 是满射
f 是单射，由 f 定义可知

群

半群

半群(Semigroup)：(S, *)，S 是非空集合，* 是二元运算，且可结合。
幺半群(Monoid)：有单位元的半群。
子半群。

幺半群的子半群未必是幺半群。例如幺半群 ({e, a}, *) 的子半群 ({a}, *) 就不是幺半群。

*	e	a
e	e	a
a	a	e

可以通过 S 的较小子集 A 来考察半群的性质。此时这个 S 的子半群 A+ 即 (A, *) 中，A 称为生成元集。称为 A 生成半群 S。
例如对半群 (Z, +)，子半群 $ {2}^+ $ 为所有的正偶数即 {2,4,6,8,...}。可以看到，这里通过列出群中所有元素的方式来描述群。

由单个元素 a ∈ S 生成的子半群 $ {a}^+ $ 称为循环子半群，a 称为生成元。如果 $ S = {a}^+ $，则称 S 是由 a 生成的循环半群。
容易发现循环半群符合交换律。

群

定义 G(a, .)：

半群
所有元素存在逆元

如果 . 可交换，则 G 是交换群，又称为阿贝尔群。
如果群中只有一个元素，称为单位元群。

设 A 是非空集合。变换群 PERM(A) 是由从 A 到 A 的全体双射函数组成的集合，它对函数复合构成一个群。由于复合运算不是可交换的，所以不是交换群。
设 A 是非空有限集合，阶为 n。则 PERM(A) 是 n 次对称群，表示为 $S_n$。
例如，当 n 为 3 时，$S_3$ 有6个元素 {p1, p2, p3, p4, p5, p6}。如下所示，这些元素的下一行是上一行的像。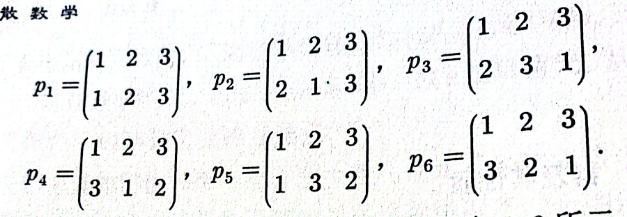

运算表如下所示

函数复合`.`	p1	p2	p3	p4	p5	p6
p1	p1	p2	p3	p4	p5	p6
p2	p2	p1	p6	p5	p4	p3
p3	p3	p5	p4	p1	p6	p2
p4	p4	p6	p1	p3	p2	p5
p5	p5	p3	p2	p6	p1	p4
p6	p6	p4	p5	p2	p3	p1

$S_n$ 的子群常称为置换群。

$(I_n, +_n)$ 是一个群。定义加法为
$$
n +_p m = (n + m) mod p
$$
譬如 n 为 3，则 $(I_3, +_3)$ 为

$+_3$	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

置换群的记法

https://zh.wikipedia.org/zh-hans/%E7%BD%AE%E6%8F%9B

群的性质

除单位元群外，群不含零元
假设存在零元 θ，则根据单位元 e 的定义有
$$
θ . θ^{-1} = e
$$
而根据零元的定义，有
$$
θ . θ^{-1} = θ
$$
所以 e 等于 θ。根据单位元的定义，可以得到任意元素 x 等于 θ。
对于群中任意元素 a 和 b，a . x = b 和 y . a = b 都存在唯一解
群满足消去律
群除了单位元外，不含有其他等幂元
设 x 是等幂元，则 x^2 = x。则 x^2 = x . e。则 x = e。
在群的运算表的任一行或者列中，群中的每个元素必然出现恰好一次
满足消去律的半群是群

循环群

群 G 中，a ∈ G，如果存在正整数 n，使得 a^n = e，则 a 的阶/周期有限，定义为 n。如果不存在 n，则 a 的阶/周期是无限的。

将 a 的周期写作 $ |a| $，即 $ |a| = min \{ k \in Z^+ | a^k = e \} $。

例如在整数加法群中，单位元 0 的周期为 1，元素 1 的周期是无限的。因此这里需要区分 a 的阶和群的阶。

元素周期的性质：

只有单位元的周期是1
群中任意元素 a 和它的逆元的周期相同
有限群 (G, .) 中每个元素的周期有限，且不大于群的阶 n = |G|
对于任意元素 a，$\{a, a^2, … a^{n+1}\}$ 中必定有两个相同元素，记为 $a^j$ 和 $a^k$。
考虑 $ a^{j-k} $，如果能证明它为单位元，则命题得证。
于是有 $ a^{j-k} = a^j . a^{-k} = a^k . a^{-k} = e $。

群 G 中如果存在 $ a \in G $，使得 $ G = \{ a^k | k ∈ Z \} $，则 G 为循环群。a 为生成元。这个可以参考循环半群的定义。

(Z, +) 是无限阶循环群，且生成元为1或者-1。

和半群一样，循环群一定是交换群。
但反过来未必成立，如 Klein 四元群是交换群，但 a、b、c 都不是生成元：

*	e	a	b	c
e	e	a	b	c
a	a	e	c	b
b	b	c	e	a
c	c	b	a	e

循环群的性质：

$ G = \{a^0, a^1, …, a^n-1 \} $，其中 n 是阶，a 是生成元。
阶相同的循环群同构
设(G, +) 和 (T, *) 阶相同，且生成元分别为 a 和 b。
如果 G 和 T 都是无限群。定义同态映射 $ h(a^i) = b^i $。
如果 G 和 T 都是有限群。定义类似的映射，但是要限定 i 小于等于 n - 1。

可以得到下面的推论，即任何循环群或者与 (Z, +) 同构，或者与某个 $(I_n, +_n)$ 同构。

子群

只含有单位元的子群，以及群 G 本身是群 G 的平凡子群。

群 G 的非空子集 H 成为子群的充要条件，是下列之一成立：

对于任意的 $ x,y \in H $，有 $ x . y \in H $；且对于任意的 $ x \in H $，其逆元属于 H。
对于任意的 $ x,y \in H $，有 $x . y^{-1} \in H $。
如果 H 是 G 的非空有限子集，则 H 对 G 的运算封闭。

子群的性质：

如果 G 是交换群，则它的任一子群也是交换群。
群 G 的任意多个子群的交集仍然为 G 的子群。

有关循环群子群的性质：

群 G 中任意元素 a 生成的循环群是 G 的子群。
循环群的子群是循环群。

可以仿照半群的概念构造群的生成元集，只是要注意加入逆元。

群的同态

如果 f 是从 (G, +) 到 (T, *) 之间的映射，且 $ \forall a, b \in G, f(a + b) = f(a) * f(b)$，显然，f 是从 G 到 T 的同态映射。G 在 f 下的像记为 Im(f) 即 f(G)。

由此也有对应的单同态、满同态和同构的概念。

如果 f 是 (G, +) 和 (T, *) 之间的同态映射，则同态像 Im(f) 是 T 的子群，且

$$
f(e_G) = e_T \quad , \quad (f(a))^{-1} = f(a^{-1})
$$

首先证明子群。考虑 Im(f) 中的两个元素 f(a) 和 f(b)

$$
f(a) * f(b) = f(a + b) \in f(G)
$$
因此运算封闭。

显然 Im(f) 对右边的运算满足结合律。

然后证明左边的等式，即 Im(f) 中存在单位元。我们还能看到同态映射将 G 的单位元映射到 T 的单位元。

$$
f(e_G) = f(e_G + e_G) = f(e_G) * f(e_G) = e_T
$$

两边右乘 $ f(e_G)^{-1} $，有
$$
f(e_G) * f(e_G) * f(e_G)^{-1} = f(e_G) * f(e_G)^{-1}
$$

考虑到 $f(e_G) \in T$，则有
$$
f(e_G) * e_T = e_T
$$

然后证明右边的等式，即 Im(f) 中存在逆元。我们还能看到同态映射将 G 的逆元映射到 T 的逆元。
$$
f(e_G) = f(a + a^{-1}) = f(a) * f(a^{-1}) = e_T
$$

考虑 $(G, +)$ 到 $(T, *)$，令 $ K = \{ x | x \in G, f(x) = e_T \}$，则 K 是 G 的子群，且 K 是同态 f 的核，记作 $ Ker(f)$。
和上面证子群的方式不一样，这里我们只需要证明
$$
\forall x, y \in K, x + y^{-1} \in K
$$
有
$$
f(x + y^{-1}) = f(x) * f(y^{-1}) = f(x) * f(y)^{-1} = e_T * e_T^{-1} = e_T \in Im(f)
$$

根据 K 的定义，因为 $ x + y^{-1} \in G $ 且 $ f(x + y^{-1}) = e_T $，则 $ x + y^{-1} \in K $。

群同态是单同态的充要条件是它的核是由单位元组成的单元素集。

必要性，左证右。因为是单同态，所以 $ e_T $ 在 G 中只有一个原像 $ e_G $，即 $ Ker(h) = \{ e_G \} $。

充分性，右证左。思路是假设 $ \exists a, b \in G, h(a) = h(b) $，证明 $ a = b $。
$$
h(a + b^{-1}) = h(a) * h(b^{-1}) = h(a) * h(b)^{-1} = e_T
$$
根据核的定义，有 $ a + b^{-1} \in Ker(h) $。而因为 $ Ker(h) = \{ e_G \} $，所以 $ a + b^{-1} = e_G $。即 $ a = b $。

设 (G, +) 是群，(H, *) 是代数系统，如果存在从 G 到 H 的满同态 f，则 H 是群。
这个是证明四要素：

结合律
单位元
逆元

Caylay 定理：任一群和它的变换群的子群同构。

基本思路是建立从 (G, *) 到它的变换群 (PERM(G, .)) 的单同态 λ，使得 G 和 λ(G) 同构。由上面的定理得到 λ(G) 是 PERM(G) 的子群。注意变换群的运算一定是函数复合。

需要注意，G 是关于某个元素 g 的群，而变换群是双射函数 g -> g 的集合。我们要找的单同态是要将任意一个 x 映射到某个函数的映射。因此先要构造这个映射。 $ \forall g \in G $，定义 $ \lambda: G \rightarrow PERM(G) $。令 $ \lambda(g) = g’ $，其中 $ g’ $ 定义为 $ g’(x) = g * x, \forall x \in G $。

首先要证明 $ g’ \in PERM(G) $。首先，因为 $ g * x \in G $，所以 g’ 是从 G 到 G 的映射。下面我们要证明这个映射是双射，也就是这个函数有逆函数/反函数。也就是要找到 $ g’ $ 的反函数 $ (g’)^{-1} $。

不妨考察函数 $ (g^{-1})’ $，我们证明它就是 $ (g’)^{-1} $。证明如下
$$
(g . (g^{-1})’) x = g . ((g^{-1})’ x) = g.(g^{-1} * x) = (g . g^{-1}) x = x
$$
可以看到 $ (g . (g^{-1})’) $ 是恒等函数，同理 $ ((g^{-1})’ . g) $ 也是恒等函数。
所以 $ (g^{-1})’ $ 就是 $ (g’)^{-1} $ 的反函数。这也证明了 $ g’ $ 是双射。$ g’ \in PERM(G) $。

下面证明 λ 是同态映射，也就是要证明 $ \forall g, h \in G, \lambda(g * h) = \lambda(g) . \lambda(h) $。不妨直接往下写
$$
\lambda(g * h) x = (g * h)’ x = (g * h) * x = g * (h * x) = g * h’(x) = (g’ . h’) x
$$
根据 λ 函数的定义，右边的 $ (g’ . h’) $ 实际上就是 $ \lambda(g) . \lambda(h) $。

下面证明 λ 这个同态映射还是单射。

NOTE 这里有点意思的地方是 $ g’ $ 和左陪集的定义有点像，特别是如果直接令 H 为 G 的话。

陪集

考虑群 $(G, .)$，H 是 G 的子群，x 是 G 中的任意元素，则子群 H 在 G 中关于 x 的左陪集(Coset) 定义为

$$
H . x = \{ h . x | h \in H \}
$$

这里的 . 可以省略。
也就是用 H 里面的每个元素，都和 x 运算一下。

还可以：在 G 上定义等价关系~

$$
\forall a,b \in G, a \sim b \iff \exists h \in H, a = b . h
$$

这个关系还可以写成
$$
\forall a,b \in G, a \sim b \iff b^{-1} . a \in H
$$

这个等价关系~给出的等价类是 H 的左陪集。其实我这里没懂，关于谁的等价类？

陪集的直观意义。一个群 G 对于一个子群 H 的每个陪集 xH 都是一个等价类，我们可以通过陪集划分群的元素。

左陪集的性质，右陪集同理：

$ \forall a \in G, a \in aH $
也就是 G 中任意元素 a 属于它的左陪集。
首先因为 H 是 G 的子群，所以单位元 e ∈ H。
然后 a = a . e ∈ aH。后面来自于陪集的定义。
$ eH = H $
子群 H 关于单位元 e 的陪集是它自己。这个其实把 eH 的定义 $ \{ e . h | h \in H \} $ 就看出来了。
不过证明集合相等还需要严格证明互相包含。
$ a \in H \iff aH = H $
从右到左好证，只要注意 e 在 H 里面就行。
从左到右，可以构造 $h = a . a^{-1} . h = a . (a^{-1} . h)\in aH $，证明 $ H \subseteq aH $。反过来显然。
$ b \in aH \iff aH = bH $
$ aH = bH \iff a^{-1} . b \in H $
$ \forall a, b \in G, aH = bH \lor aH \cap bH = \emptyset $
aH 和 bH 要么完全相同，要么毫无共同元素。因此我们可以通过左陪集去划分一个群。
这个可以看下面定理的证明的一部分。

群 G 的一个子群 H 的右陪集 Hx 构成群的一个划分：
首先，G 中任意元素至少属于 H 的一个右陪集。这个简单，根据左陪集的性质1，可以得到任意元素 a 属于 Ha。所以 G 是 H 的不同陪集的并。
下面只要证明上面的性质6，也就是这些集合不相交，那么就能得到一个划分了。这里的思路是先证明 $ \forall z \in H x, H . z = H . x $。然后我们设 $ z \in (Hx) \cap (Hy) $，则 $ Hz = Hx $ 且 $ Hz = Hy $，显然 $ Hx = Hy $。性质6得证。

要证明 $ \forall z \in H x, H z = H x $，不妨先证明 $ Hz \subseteq Hx $，然后用同样的办法证明 $ Hx \subseteq Hz $ 就行了。

首先 $ z \in Hx $，它实际是说 $ \exists h \in H, h . x = z $。那来看看 $ Hz = \{ h_2 . z | h_2 \in H \} $。然后我们就可以带入

$$
h_2 . h . x = (h_2 . h) . x
$$

因为 $ h_2 . h \in H $，所以对于 $ Hz \subseteq Hx $。

设 H 是 G 的子群，$ x \in G $，f(h) = h.x 是从 H 到 Hx 的函数，则 f 是双射。
首先，这个 f 实际上就是从 H 构造右陪集 Hx 的函数。
先证明是满射。也就是 $ \forall k \in H x $，都能找到一个它的原像。不妨设 $ k = h . x $，则 $ h = k . x^{-1} $。现在验证这个 h 确实是 k 的原像。有

$$
f(h) = f(k . x^{-1}) = k . x^{-1} . x = k
$$

再证明是单射。也就是对于任意的 h1 和 h2，如果 f(h1) = f(h2)，则 h1 = h2。只要展开来就发现可以约掉了，从而得证。

这个定理说明了，右陪集 $Hx$ 有 $|H|$ 个元素。

拉格朗日定理：
$$
|G| = |G / H| |H|
$$

这个很简单，根据上面的定理，右陪集 $Hx$ 有 $|H|$ 个元素。根据之前的性质6，H 的陪集构成对 G 的划分。

拉格朗日定理有几个推论：

有限群 G 的每个元素 a 的阶/周期都是 G 阶数的因子
因为 $({a}, .)$ 是 G 的子群，根据拉格朗日定理，$ |\{a\}| $ 是 $|G|$ 的因子。
因为 $|a|$ 有穷，所以 $ |\{a\}| = |a|$。
注意，这里 $(\{a\}, .)$ 未必只有一个元素。
设 H 是有限群 G 的子群，则 H 的阶整除 G 的阶
这个显然，$ |G| / |H| = |G / H| $。
阶数为素数的群必然是循环群
循环群的定义是 $ G = \{ a^k | k \in Z \} $。
一种思路是要不 $ |G/H| $ 是 1，要不 $ |H| $ 是 1。到底谁是1呢？
不妨考虑先证明素数阶的群的子群只有平凡子群 $\{ e \}$，和 G。根据上面的定理，子群 H 的阶需要能整除 G 的阶。而因为 |G| 是素数，所以子群 H 的阶只能是 1 或者 |G|。
循环群只有平凡子群，没有真子群
就是上面一个。

正规子群

设 H 是群 G 的子群，对 $ \forall x \in G $，有 $ x . H = H . x $，则 H 是 G 的正规子群。记作 $ x \lhd y $。

H 是正规子群的充要条件：

$ \forall a \in G, \forall h \in H, aha^{-1} \in H $
$ \forall a \in G, aHa^{-1} = H $
$ \forall a \in G, aHa^{-1} \subseteq H $

设 $h$ 是从 $(G, .)$ 到 $(T, *)$ 的同态映射，则：

核 $Ker(h)$ 是 $G$ 的正规子群。
$\forall x \in G, K . x = \{ z | z \in G \wedge h(z) = h(x) \} $。
这个性质进一步推动后续对商群的理解。它是在说核 K 在 G 中关于 x 的右陪集 $ K . x $ 中的所有元素，通过同态映射 h 都能得到一样的像。
这样我们自然而然想到，给定一个子群，是不是可以把陪集“约”掉呢？

要证明 $ xK = Kx $，就是要证明 $ Kx \subseteq xK $，然后再同理。而前者就是要证明 $ \forall x \in K, kx \in xK$。
这里一个技巧是，因为 $ xK $ 是 $ \forall x \in K, x.k $ 构成的集合，所以我们要想办法凑一个 x 出来。怎么办呢？

$$
kx = x (x^{-1} k x)
$$

所以只需要证明右边 $ x (x^{-1} k x) \in K $。其实通过第二个充要条件就能直接走到这一步。有
$$
h(x^{-1} k x) = h(x^{-1}) * h(k) * h(x)
$$
根据先前的定理，右边等于
$$
h(x)^{-1} * h(k) * h(x)
$$
根据核的定义，因为 $ k \in K $，所以还可以f化为
$$
h(x)^{-1} * e_T * h(x) = e_T
$$

商群和同态定理

最终，我们呼之欲出的是对商群的定义。
设 $K$ 是群 $(G, *)$ 的正规子群，则

在 $G$ 中 $K$ 全体陪集的集合 $ G/K $ 中定义运算 $ \otimes $ 为 $ (K * x) \otimes (K * y) = K * (x * y)$，则 $ (G / K. \otimes) $ 是一个群，称为 G 对 K 的商群。
定义从 $G$ 到 $G/K$ 的映射 $\gamma(x) = K * x $，它是一个同态映射，且核为 $K$。称为从群 $G$ 到商群 $G/K$ 的自然同态。

注意，这里的 $G/K$ 实际上是个集合的集合。

关于第一个结论，书中花了好多篇幅介绍定义运算 $\otimes$ 的合理性。即如果 $K * x = K * x’ \wedge K * y = K * y’$，则 $ (K * x) \otimes (K * y) = (K * x’) \otimes (K * y’) $。这里估计是要证明如果 $a=a’ \wedge b=b’$ 则 $ a \otimes b = a’ \otimes b’ $。

实际上，就是要证明 $\otimes$，在 $ G/K $ 上是可结合的，$ K * e $ 是单位元，且 $ (K * x)^{-1} = K * x^{-1} $。

关于第二个结论，根据 $\otimes$ 的定义，可以直接证明 $\gamma$ 是一个同态。
下面需要证明 $G$ 的正规子群 $K$ 是 $ \gamma $ 的核。这个核是什么？根据定义以及 $K$ 是 $G/K$ 的单位元，可知
$$
Ker(\gamma) = \{ x | x \in G \wedge \lambda(x) = e_{G/K} = K \}
$$

而如果 $ \forall x \in G, \gamma(x) = K * x = K $，因为 $ K * x = K $，根据子群的性质，有 $ x \in K $。

反之 $ \forall x \in K$，则 $ K * x = K $，则 $ \gamma(x) = K * x = K $，所以 $K$ 是 $ \gamma $ 的核。

同态基本定理：设 $h$ 是从 $ (G, .) $ 到 $(T, *)$ 的同态映射，$K$ 是同态核，则商群 $ G/K $ 在 $ h^* $ 下与 $ h(G) $ 同构，此处 $ h^*$ 为
$$
h^*(K . x) = h(x)
$$

先证明 $h^*$ 是同态。那是要证明啥呢？还是先列一下条件：

$ h^* $ 是从 G 的陪集到 T 的某个元素的映射。实际上就是将 $K . x$ 这个陪集映射到 $ x $ 上。
首先有一个从 G 到 T 的同态 h，核 $ Ker(h) $ 令为 K。因为 G/K 是商群，所以 K 是正规子群。
商群 $ G/K = (\{ H.x | \forall x \in G \}, \otimes) $，那么要证明它同构于 $h(G)$，也就是 G 在 f 下的像。

因此就是要证明 $ h^*((K . x) \otimes (K . y)) = h^*(K . x) * h^*(K . y) $。证明过程很简单，套定义就行了。

然后还要证明 $h^*$ 是单射，也就是要证明如果 $ h^*(K . x) = h^*(K . y) $，则有 $ K . x = K . y$。这里书上说根据定理 4.29 就得证。

我觉得是根据 4.28(2) 即 $\forall x \in G, K . x = \{ z | z \in G \wedge h(z) = h(x) \} $ 得证的。
因为
$$
\forall x, y \in G, h(x) = h(y)
$$
那么可以看出 $K . x$ 和 $K . y$ 两个集合是相等的，即
$$
\{ z | z \in G \wedge h(z) = h(x) = h(y) \}
$$