相对于序列,字符串一定是连续的,字符串匹配和查找算法,如KMP、Trie、AC自动机等是比较基础的串算法。并使用摊还分析等方法分析了部分算法的复杂度
KMP
KMP算法是一种前缀搜索方法,也就是说在搜索窗口内从前向后逐个读入文本字符,搜索窗口中文本和模式串的最长公共前缀。相对于前缀搜索,还有后缀搜索(Boyer-Moore、Horspool、Sunday)、子串搜索等方法。
为了方便阅读,未特别注明情况下统一模式串为P,长m,以j为下标;文本串为S,长n,以i为下标,i和j下标从0开始。(i,j)表示匹配S[i]和P[j]。
KMP对朴素算法的优化
- 朴素的字符串匹配算法复杂度为
O(n*m),对于长n的文本串S,从位置[0..(n-m)]开始搜索匹配长m的模式串,对于每个位置至多需要m次比较。假设在(i,j)位置发生失配,那么接下来应当从(i-j+1,0)位置开始重新匹配。 - 容易发现其中有一些比较和回退操作是多余的。例如,假定模式串为
P为'ABCDABD',文本串为S='ABC ABCDAB',假设从(0,0)位置开始匹配,在(3,3)位置发现' '和'D'不等。此时朴素算法直接在(1,0)位置重新开始匹配,但实际上在刚才比较过程中可以得到(0..3,0)位置都是不行的,因为'B'、'C'、' '都不等于'A',因此可以从(4,0)重新开始匹配。 - 另一个例子,考虑新的S=
'ABCDAB ABCDABCDABDE',在(6,6)处发现' '和'D'不等失配。同时发现P[0..1]和P[4..5]都能匹配S[4..5](当然S[4..5]和S[0..1]都能匹配P[0..1]的'AB',但目前我们考虑只移动模式串),由此可以尝试从(4,2)(注意j变成了2不是0)开始重新匹配,容易发现S并没有发生回退,而P右移了4位,用自己P[0..1]而不是P[4..5]的'AB'去匹配S[4..5]了。 - 因此可以得到KMP算法的思想:如果模式串
P在(i,j)处失配文本串S,那么可以知道至少P[0..(j-1)]和S[i..(i+j-1)]是匹配的,既然如此,不妨可以利用已经匹配的这段长度,只回退(将串向右移动)模式串P,不回退文本串S(注意在KMP算法过程中对文本串S的操作只有递增一个)。因此通过KMP算法,假设在(i,j)位置发生失配,那么接下来应当右移符号串j-f(j)长度,从(i,f(j))位置开始重新匹配(注意此时失配前P[0..(j-1)]和S[i-(j-1)..i-1]已经匹配的部分会和P[f(j)-(j-1)..f(j)-1]重新匹配),其中f为next函数,将在下节中详细介绍;特别地,当j = 0时,我们应当从(i+1,0)开始匹配。可以得到这样算法的复杂度为O(n+m)。
KMP算法和next函数
首先定义边界的概念,串v是串u的边界表示串v是串u的后缀,也是串u的前缀。我们考虑一下这样的u,它是一个奇妙的字符串,它的最前面一段和最后面一段是可以重叠的。
有两类函数可以实现KMP,一种是fail函数fail(j),对于失配的(i,j),fail(j)是P[0..j]中最长边界对应的前缀的最后一个元素的下标。另一种是next函数next(i),对于失配的(i,j),next(j)是P[0,j-1]中最长边界后面那个元素的下标。这里的定义很奇怪,这是由于我们是从如何计算而不是如何应用的角度来说的。从作用上来讲,next(j)表示在(i,j)失配后rewind模式串(右移),从(i,next(j))重新匹配。fail实现的特点是计算的值会有很多-1,但是next实现只有next(0)是-1。在这里我们采用next函数进行描述。
- next函数
f(j)指出了查找下一个匹配时的模式串(这里可以理解为P[0..m-1]的子串P[0..j])的回退距离(模式串P向右移动的距离),或者可以被称作最长边界。用形式方法来描述即,对于模式串P[0..j]来说,f(j)=max(k),这里k满足P[(j-1)-(k-1)..(j-1)]即P[(j-k)..(j-1)]=P[0..(k-1)](注意这里是j-1和k-1,在别的定义/实现方式中可能使用j和k)。
这里要求是最大的k也就是最长边界,原因是考虑到可能存在多个k,为了不丢失匹配,回退距离应当尽可能小。 - 特别地,当
j = 0时,即对于(i,0)位置的失配,指定f(0)=-1,这意味着我们应当递增文本串S的指针i,从下一位置匹配。 - 为了计算所有的
f(1..m),可以根据定义进行计算,朴素的方法需要O(m^2)的复杂度。但是可以采用dp实现线性复杂度的算法:
令f(j)=k,即已知最大的k满足P[j-k...j-1]=P[0...k-1],现在求**f(j+1)**:- 如果
P[k]=P[j],则f(j+1)=k+1。 - 如果
P[k]!=P[j],于是显然P[0..k]显然不是P[0..j]的后缀(注意根据f定义下标分别是到j和k),所以只能在P[0..(k-1)]上寻找P[0..j]的后缀,但是P[0..(k-1)]也不一定就满足条件,当然可以对P[0..(k-1)]的所有前缀判O(k^2)次,但是也有简单办法,那就是利用失配前已经匹配了的结果。请在这里停顿并尝试自己推一下下面的过程,并体会其中的奇妙之处。
令k=k2=f(k),继续寻找,如果此时P[k2]=P[j],那就符合了,否则还要继续寻找。为什么说只要比较P[k2]=P[j]就行了呢?前面的k-1的长度不需要比较了么?因为k2是最大的满足P[k-k2..k-1]=P[0..k2-1](也就是P[0..k2-1]的最长边界长度),而注意到我们发现P[k]!=P[j],说明至少P[0..k-1]和P[j-k..j-1]是匹配的,因此P[0..k2-1]=P[k-k2..k-1]=P[j-k..j-1],即我们新找到的P[0..k2-1]也和P[j-k..j-1]匹配。
- 如果
- 下面对
P='ABCDABD'构造next函数。根据上文,首先有f(0)=-1。接下来计算f(1),也就是在(i,j = 1)发生失配。我们需要找到此时P[0..(j-1)]='A'的某个后缀同时也是P的前缀,显然并不存在。
简单的总结下,我们DP的过程是,假设已经求得P[j],便尝试通过匹配的P[0..a] = P[b..j]来推导P[0..a+1]和P[b-1..j+1]是否匹配,如果P[a+1] != P[j+1]就可以立马使用前面的P。
为什么要从a推到a+1而不是从a-1推到a
我们看到上面的递推过程是从next[a]推到next[a+1],为什么不能从next[a-1]推到next[a]呢,这看起来更像常见的DP啊。我们不妨测试一下,设dp[j]为P[..j] == P[0..k]最大满足的k。
1 | dp = [0 for i in xrange(n)] |
我们发现不加上上面的注释的时候代码会死循环,这是因为当k == 0时dp[k - 1]越界了。而加上注释那么所有的dp都会变为0。仔细思考,这是因为我们不能区分0位置处是否能匹配的缘故。所以我们的next是失配指针,next[0]指的是0位置失配,而next[1]指的是1位置失配,此时0位置是匹配的。
求next函数和KMP算法比较
KMP算法实际上是求模式串P[0..m]对文本串S[0..n]长度为m+1的边界(如果存在即找到)。
next函数实际上是求模式串的某个前缀P[0..j]对P[0..j]长度最大的边界。
回想KMP算法,在(i,j)位置发生失配,那么接下来应当从(i,f(j))位置开始重新匹配,因为f(j)是P[0..(j-1)]的最长边界。而在计算next函数f(j+1)时候,如果P[k]!=P[j],那么可以理解为模式串P[0..k]在匹配文本串P[0..j]时在(j,k)发生失配,因此同样可以利用之前已经匹配了的结果,按照KMP应当从(j,f(k))开始寻找。
相关资料
KMP算法有很多教程,每个教程都给出了自己的一套理解方法,没有一个我能够完全看懂。在学习过程中,我参照了Wikipedia的解释,其中适当后缀(proper suffix),指的是不是自己本身的后缀,也就是“真后缀”。
1 | // kuangbin模板 |
我也写了个实现
复杂度分析
求next函数具有线性复杂度,考虑到内部有一层while,使用通常方法不易计算。实际的复杂度计算使用了摊还分析。
摊还分析
对于一个操作序列,并不是所有操作的复杂度都相等的,例如对于std::vector,push_back()操作是O(1)的,但是当满了之后resize的操作却是O(n)的,仅通过push_back()便认为对std::vector增加一个元素需要常量时间是不恰当的(虽然却是是常量时间)。摊还分析(amortized analysis)是一种分析操作序列中所有操作的平均时间上界的方法。摊还分析主要有聚合法,核方法和势能法。
聚合法
聚合法就是求出所有操作加起来最坏情况的总代价,然后除以总操作数。对于std::vector的添加元素操作来说,假设初始大小是1,倍增因子是m,要添加$n$个元素,需要重新分配内存$\lceil log_{m}{n} \rceil$次,第$i$次分配内存需要移动$m^{i-1}$个元素,总共需要$ \sum_{i=1}^{\lceil log_{m}{n} \rceil}{m^{i-1}} = O(n) $次移动操作,另需要push_back $n$次。因此复杂度为O(1)核方法
MIT的算法导论课公开课老师讲这个的时候在黑板上写了2 3 3 3…对这个记忆犹新
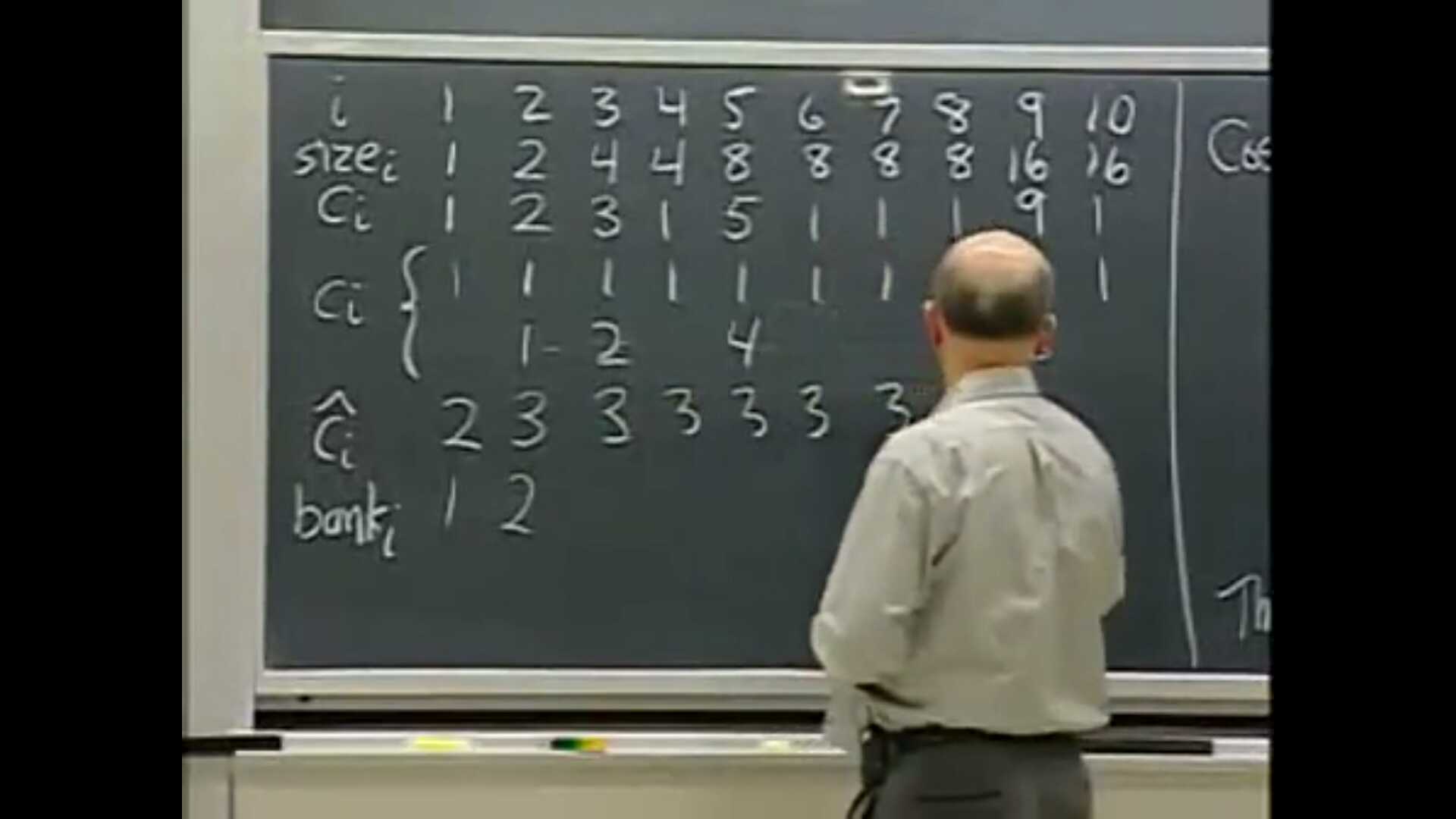
核方法的原理就是把复杂度低的操作承担一部分复杂度高的操作的代价,从而证明算法复杂度的上界。定义$c_i$为第$i$个操作的真实代价,定义$\hat{c}_i$为摊还代价。在第$i$时刻,定义信用为$\sum_{i=1}^n{\hat{c}_i} - \sum_{i=1}^n{c_i}$,选取的摊还代价要保证信用始终非负,因为一旦信用是负数,那么这个操作实际上是在开销上界内不能完成的
上图是一个倍增因子m为2的动态表std::vector,$size_i$表示添加第$i$项时的表达大小,真实代价$c_i$由两部分组成,一部分是添加进表的固定成本($c_i$第一行),另一部分是把元素复制到新表中的成本($c_i$第二行),$bank_i$就是信用。对于$m=2$的情况,可以发现$\hat{c}_i$取3即可,这包括自己的真实代价,移动表的前一半的代价,和移动表的后一半的代价。对于普遍的倍增因子m,后面m-1的元素要m个元素的移动代价,加上添加进表的1,摊还代价取$1 + \frac{m}{m - 1}$,特别地$i = 1$时只要支付自己的移动代价,故摊还代价为$1$,于是等式左边$\sum_{2}^{n}{(\frac{m}{m - 1})} + n = \frac{2nm - n - m}{m - 1} $,等式右边$n + \sum_{0}^{\lceil log_{m}{n} - 1 \rceil}{m^i} = n + \frac{n - 1}{m - 1} = \frac{nm - 1}{m - 1}$,发现左边恒大于右边。势能法
势能法和核方法基本上是相同的,区别在于核方法要先假设摊还代价,而势能法先考虑的信用和(也就是势)。对于有的题目势能法比核方法简单。对于上面的$m=2$的动态表,定义势函数$\phi(D_i) = 2i - 2^{\lceil log_{2}{i} \rceil}$,由于$i = 2^{log_{2}{i} }$,所以可以得到式子恒为正。因此满足势函数的基本要求$\phi(D_0) = 0$和$\phi(D_i) \ge 0$。下面计算摊还代价$\hat{c}_i = c_i + \phi(D_i) - \phi(D_{i - 1}) $,其中$c_i = \begin{cases} i \, , \, (i - 1) & ((i - 1) - 1) == 0 \\1 \, , \, otherwise \end{cases}$。通过对$i$的讨论,可以发现每个操作的摊还代价是3,这和前面的核方法形成了印证。
下面考虑倍增因子为m的情况,定义势函数为$\phi(D_i) = 2i - m^{\lceil log_{m}{i} \rceil}$,可以进行类似的计算,得到每个操作的摊还代价是$1 + \frac{m}{m - 1}$
求next函数的复杂度
下面使用摊还分析计算求next的kmp_pre函数的复杂度。首先跟踪变量k,因为k出现在了最内层的while中,但是j没有出现。发现对k有两次操作,第一个是k = f[k],这个操作是当P[k] != P[j]时,利用先前的结果计算f(j+1)。第二个是++k,这个是当(j, k)匹配时,令f[j + 1] = k + 1,并继续外层的while循环循环计算f(j + 2)的值,直到j >= m结束,m是模式串的长度。
可以发现外层的j和k每次自增1,并且在等于m的时候跳出循环,这类似于对动态表添加元素的1的代价。特别地可以发现j和k的上界最高就是m。
内层while循环是将k不断缩小,很难求出外循环的某次循环中内循环共循环了多少次,但是可以看出内循环体在整个函数中最多被执行m次,这是因为k最多只能加到m,所以最多只能变小m次。将外层循环视为操作序列,内层循环摊还的代价就是$O(1)$。因此这个函数的总代价是线性的。
Trie
Trie(/ˈtraɪ/,字典树,前缀树)将多个字符串组成一棵有序树。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。在构造Trie树时,需要用flag数组标记每个节点是否可能是某个字符串的结尾,而不能仅靠“无路可走”来断定,例如对于单词表[b, bb],b和bb都是合法的单词。
例题
HDU 1247是Trie的简单应用,首先把每个字符串添加到Trie树上,然后对于每个字符串,搜索他的每个前缀,对于任意前缀,如果它产生的字符串属于这个单词表(碰到flag为true的节点),那么紧接着继续往下搜索看能不能搜到第二个字符串。这道题注意要搜索每个前缀,考虑下面的样例
ha
hat
word
hatword
如果在实现时,对hatword第一次query到ha即返回,下面从tword开始就无法匹配了,由于第一次query已返回,所以也不会继续搜索前缀hat了。
AC自动机
AC自动机(Aho-Corasick automation)能够匹配多个字符串,可以用来在线性时间内解答字符串S中出现了哪些字典D中的模式串的问题。从算法思想上来看,AC自动机结合了Trie和KMP的思路,虽然它的出现甚至要比KMP早。对我来说AC自动机的思想显得比KMP“自然”点,我们在Trie树上走,如果走不下去(失配)了,我们就回退到某个上层的节点。在这点上和KMP很相近,因为KMP也不回退文本串。
于是现在我们要高效的求出在失配时是需要回退到的节点,也就是为所有节点生成失配指针。显然我们的高效算法能够利用先前节点的结论,所以我们以BFS的顺序来访问这个树上的所有节点。首先root的失配指针肯定是NULL,root都失配那就无路可走了。我们按照下面的规则生成失配指针,假设从状态S1通过读取字符x可以到达状态S2,我们现在计算状态S2上的失配指针。首先我们查看S1的失配指针指向的状态节点F1,注意F1不一定是S1的父节点,有可能在Trie的另一个分支上,所以我们需要BFS而不是DFS。接下来我们查看F1能不能通过x走到它的一个儿子节点F2,如果能,那么就更新S2的失配指针为F2,如果不能我们就沿着这个F1的失配指针继续网上找。容易看出现在root的前缀指针None显得不太合群了,因为root所有的子节点的失配指针都应当是root,而按照上面的规则会被计算成是自己。
后缀数组
字符串S[0..n-1]后缀是指的形如S[i..n-1]的字符串。后缀数组P[0..n-1]给出了S的所有后缀S[i..n-1]经过字典排序后的起始下标i。

