本文从MIT的线代教程的角度重新学习线性代数。
这是第三部分,从 L26 开始。
L26 对称矩阵和正定矩阵
本章讲对称矩阵。
这里注意,因为对称矩阵不一定满秩,比如
$$
\begin{equation}
\begin{bmatrix}
1&1 \\
1&1
\end{bmatrix}
\end{equation}
$$
就不满秩。
首先介绍实对称矩阵,有两个特性:
- 特征值都是实数
- 特征向量正交
这里注意,如果出现重特征值,则可能一个平面中都是特征向量。所以这里说的是总能选出一套完全正交的特征向量。
其实这里我不是很懂,投影矩阵是个什么样的例子呢?
在 L22 已经讲过如何判断是否存在 n 个线性无关的特征向量了。现在假设存在,那么矩阵可以对角化为 $A = S \Lambda S^{-1}$。
对对称矩阵进行对角化,因为特征向量正交,所以 S 实际是正交矩阵,这里改写为 Q。因为 Q 是正交矩阵,根据正交矩阵的性质,有 $Q Q^T = I$,即 $Q^{-1} = Q^T$。所以有
所以可以得到下面的式子。
$$
A = Q \Lambda Q^{-1} = Q \Lambda Q^T
$$
上面的定理又被称为谱定理或者主轴定理。
在笔记上还写了一段
下面来证明为什么实对称矩阵的特征值都是实数。特别地,第二个性质教授说直接看课本就行。
首先他介绍了一个特性,其中 $\overline{c}$ 表示复数 c 的共轭。
$$
\overline{A} \overline{x} = \overline{\lambda} \overline{x}
$$
考虑上面的式子,可以得到
$$
\overline{x}^T \overline{A}^T = \overline{x}^T \overline{\lambda}
$$
考虑到 $\overline{A} = A$ 和 $A = A^T$ 可以得到
$$
\overline{x}^T A = \overline{x}^T \overline{\lambda}
$$
两边同时右乘 x 有
$$
\overline{x}^T A x = \overline{x}^T x \overline{\lambda}
$$
接下来考虑 $ A x = \lambda x$,两边同时左乘 $\overline{x}^T$ 有
$$
\overline{x}^T A x = \lambda \overline{x}^T x
$$
比较可得,$\overline{\lambda} = \lambda$ 或者 $\overline{x}^T A$ 为0。下面要证明后者不为0。
不妨展开看一下
$$
\begin{equation}
\begin{bmatrix}
\overline{x_1}&…&\overline{x_n}
\end{bmatrix}
\begin{bmatrix}
\overline{x_1} \\
… \\
\overline{x_n}
\end{bmatrix}
\end{equation}
$$
其中每一个 $\overline{x_i} x_i$ 都可以看做是 $(a + bi)(a - bi)$,结果为复向量的模。只有当向量是0的时候,模才是0。
特别地,如果 A 是复矩阵,那么要满足上面两个条件则需要 $ A = \overline{A}^T$。
TODO
下面介绍一个性质,也就是主元的符号和特征值的符号数量是匹配的。例如有 x 个主元为正,n - x 个主元为负,那么就有 x 个特征值为正,n - x 个特征值为负。
正定矩阵是对称矩阵。它的所有特征值为正。所以它对应的微分方程是收敛的。
【Q】这里为什么要在对称矩阵上定义正定矩阵呢?
正定矩阵的主元都为正。
可以通过行列式判断是否是正定。如果 A 正定,则 $det(A) \gt 0$。但反之就未必,例如矩阵
$$
\begin{bmatrix}
-1&0 \\
0&-3 \\
\end{bmatrix}
$$
其实要所有的子行列式都为正才行。
L27 复矩阵和快速傅里叶变换
我们如何定义两个复向量正交呢?$z^T z = 0$ 可以么?不行。因为 $z^T z$ 是向量模长的平方,它应该是一个正数。但如果考虑
$$
\begin{equation}
\begin{bmatrix}
1&i
\end{bmatrix}
\begin{bmatrix}
1 \\
i \\
\end{bmatrix}
= 0
\end{equation}
$$
难道向量的长度为0?
实际上我们定义复向量 z 的模是 $\overline{z}^T z$,也可以写作 $z^H z$。这里的 H 表示埃尔米特(Hermitian)矩阵的意思。
进行延伸,我们定义复矩阵中的“对称矩阵”。它被称作埃尔米特矩阵,定义为 $\overline{A}^T$ 即 $A^H$。它的特性是 $\overline{A}^T = A$。
下面的例子是一个埃尔米特矩阵,可以发现主对角线上一定都是实数,主对角线两边的元素“共轭对称”。
$$
\begin{bmatrix}
2&3+i \\
3-i&5 \\
\end{bmatrix}
$$
埃尔米特矩阵具有实数特征值和正交的特性向量,这个应该是从对称矩阵上类比得到的,教授在上节课证明的时候已经带过了。
类似地,我们定义对应于“正交矩阵”的概念即酉矩阵。
假如 $q_1$、$q_2$、……、$q_n$ 彼此标准正交,即
$$
\begin{equation}
\overline{q_i}^T q_i =
\left\{
\begin{array}{lr}
0, \quad i\ne j \\
1, \quad i=j
\end{array}
\right.
\end{equation}
$$
可以得到 $Q^H Q = I$,这里 $Q^H$ 就是酉矩阵。
求逆方便的原因是 $F_4^H F = I$,所以逆就是共轭转置。
容易想到 $F_{64}$ 和 $F_{32}$ 之间可能有联系。在 $F_{64}$ 中,w 是 1 的 64 次方根,不妨记作 $w_{64}$。可以发现 $w_{64}^2 = w_{32}$。
如何建立 $F_{64}$ 和 $F_{32}$ 之间的联系呢?不妨考虑下面的式子,$F_{64}$ 被拆成两个 $F_{32}$ 组合起来很稀疏的矩阵。
$$
\begin{equation}
F_{64} =
X
\begin{bmatrix}
F_{32}&0 \\
0&F_{32}
\end{bmatrix}
P
\end{equation}
$$
当然,整个式子要乘上 X 和 Y 才能成立。
这里的 Y 是一个奇偶置换矩阵,如下所示。从矩阵乘法的第四种方法可以看出。
而 X 是一个
$$
\begin{bmatrix}
I&D \\
I&-D
\end{bmatrix}
$$
其中 D 是对角矩阵,对角线上的值为从 $w^0$ 到 $w^{32}$。
建立上面联系的目的是什么呢?比如如果要做傅里叶变换,那么就要用 $F_{64}$ 乘以某个向量,这是 $64^2$ 的复杂度。但经过上面的分解,我们只需要 $2*32^2 + 32$ 即可。
还可以从 32 继续分解为 16/8/4/2/1。最终中间的矩阵越来越简单,但两侧会补上很多的修正矩阵。
L28 正定矩阵和最小值
首先是复习上上节课介绍的正定性的判断方法。主要分为:
- 特征值法
- 行列式法
- 主元法
这里需要注意之前讲的一个性质,也就是主元的积等于行列式的值。 - $x^T A x \gt 0$,实际上一般这才是定义
注意,这里是不是要把原点扣掉?因为令 x 为零向量,那么肯定是等于0的啊?
下面教授举了几个例子。
[2 6; 6 18] 是一个半正定矩阵。因为它是奇异矩阵,所以有一个特征值为0,只有一个主元。半正定矩阵的特征值大于等于0。
而 [2 6; 6 7]就是不定矩阵,它实际上是一个马鞍面。
[2 6; 6 20]是正定矩阵。
从微积分的角度来看,极小值点满足一阶导数为零,且二阶导数为正。这里教授说的是 minimum,不知道翻译成啥。
从线性代数中,f(x1, x2, … xn) 存在极小值的条件是二阶导数矩阵是正定的。
事实上对 [2 6; 6 20] 进行配方,得到的是 $2(x + 3y)^2 + 2y^2$,它的图像是一个碗形。它的某个截面是椭圆,其实可以从椭圆的方程就能看出来了。
其实配方法就是矩阵消元,可以从矩阵消元得到。
例如我们将矩阵 [2 6; 6 20] 进行 LU 分解。显然 U 是 [2 6; 0 2]。因为我们是用第二行减去了第一行的三倍,所以 L 是 [1 0; 3 1],也就是加回来。
什么是二阶导数矩阵呢?
其中 $f_{xx}$ 和 $f_{yy}$ 必须为正,才有最小值。并且还需要足够大以抵消混合导数的影响。
$$
\begin{bmatrix}
f_{xx}&f_{xy} \\
f_{yx}&f_{yy}
\end{bmatrix}
$$
这里 $f_{xy} = f_{yx}$,所以也能看出为什么二阶导数矩阵是对称的了。
TODO
L29 相似矩阵和若尔当标准型
正定矩阵从何而来?它实际上来自于最小二乘法。不放先复习下,这里的 A 是一个长方形矩阵。
$$
\hat{x} = (A^T A)^{-1} A^T b
$$
我们要研究在什么情况下 $A^T A$ 是正定的。
先来想一想,正定矩阵肯定是对称的。正定矩阵的逆矩阵一定也是正定的,判断正定性有四种做法,$x^T A x \gt 0$、主元、特征值、子行列式。我们知道逆矩阵的特征值是倒数,那么不影响正负号。这里补充下,对称矩阵的逆矩阵也是对称的,可以由很早之前证明的 $(A^{-1})^T = (A^T)^{-1}$ 得到。
如果 A 和 B 都是正定矩阵,那么 A + B 是正定矩阵。这个可以从第一种判定办法得到。
回到一开始的问题,也就是什么情况下 m 行 n 列的长方形矩阵 $A$,有 $A^T A$ 是正定的。直觉上来看,它像是一个数的平方,肯定大于等于0,但矩阵中是否这样呢?
我们选用第一种判定办法来研究。也就是证明 $x^T A^T A x$ 大于0。即要证明 $(A x)^T A x \gt 0$,而 $A x$ 是个向量,向量的模是大于等于0的,并且等号只在零向量取得。那么什么时候 $A x$ 为 0 呢,或者更有用的是反过来,如何保证 $A x$ 不为0呢?这样我们就取不到等号了。这个也就是在问什么时候 A 的零空间里面只有零向量,这个很简单,满秩的情况下。也就是说如果 A 满秩,那么 $A^T A$ 正定。
现在已经很接近最后的核心内容,正定性将之前的东西联系起来。
现在我们不再讨论对称阵了,而是普通的方阵。
A 和 B 是相似的,则存在某个可逆矩阵 M,有 $B = M^{-1} A M$。这个式子有什么意义?其实先前在对角化的时候就已经见到过。$S^{-1} A S = \Lambda$ 可以描述为 A 和 $\Lambda$ 相似。
【Q】其实我觉得这里只要 M 可逆就行了。
但如果我们不取特征向量矩阵 S,而是取另一个 M,同样可以得到另一个相似矩阵 B。所以所有的相似矩阵可以划为一类,并可以由其中最好的矩阵 $\Lambda$ 来代表。
例如考虑 [2 1; 1 2],它的特征值矩阵 $\Lambda$ 是 [3 0; 0 1]。但我们也可以取另一个可逆矩阵 M = [1 4; 0 1],它是上三角矩阵,可以轻松算到逆矩阵是 [1 -4; 0 1],通过 M 可以得到另一个相似矩阵。总而言之,下面的几个矩阵都是相似矩阵,可以从特征值来验证。
$$
\begin{equation}
\begin{bmatrix}
2&1 \\
1&2
\end{bmatrix}
\sim
\begin{bmatrix}
3&0 \\
0&1
\end{bmatrix}
\sim
\begin{bmatrix}
3&7 \\
0&1
\end{bmatrix}
\sim
\begin{bmatrix}
1&7 \\
0&3
\end{bmatrix}
\end{equation}
$$
所有的相似矩阵的特征值是相同的。可以给出如下的证明:
$$
A x = \lambda x \\
A M M^{-1} x = \lambda x \\
M^{-1} A M M^{-1} x = M^{-1} \lambda x \\
B M^{-1} x = M^{-1} \lambda x
$$
因此这些矩阵都具有特征值 $\lambda$。但对应的特征向量则未必一样,为 $M^{-1} x$。
【Q】不妨考虑这个问题,如果两个矩阵的特征向量都相同,那么这两个矩阵一定相同么?答案不是,可以考虑
$$
\begin{equation}
\begin{bmatrix}
2&1 \\
1&2
\end{bmatrix}
\begin{bmatrix}
3&2 \\
2&3
\end{bmatrix}
\end{equation}
$$
有
1 | np.linalg.eig(np.array([[2,1],[1,2]])) |
如果两个矩阵的特征值和特征向量都相同呢?这两个矩阵也不一定相同,可以考虑
$$
\begin{equation}
\begin{bmatrix}
2&1 \\
0&2
\end{bmatrix}
\begin{bmatrix}
2&0 \\
1&2
\end{bmatrix}
\end{equation}
$$
下面介绍一些比较难的情况。首先是有重特征值的情况,这意味着特征向量未必是线性无关的了,当然还是有可能线性无关的。但如果不存在 n 个线性无关的特征向量,那么就不能对角化。
假设有重特征值4,可以分为下面的情况:
第一种如下,和单位矩阵相关
$$
\begin{equation}
\begin{bmatrix}
4&0 \\
0&4
\end{bmatrix}
\end{equation}
$$
对于这种矩阵 $M^{-1} A M = A = 4I$。
所有其他的矩阵类似于
$$
\begin{equation}
\begin{bmatrix}
4&1 \\
0&4
\end{bmatrix}
\end{equation}
$$
不同于上面的单位矩阵,这是一个不可对角化的矩阵。这里可以看出,矩阵经过初等变换之后,可能从原来的可对角化变成不可对角化了。
这样的矩阵称为若尔当标准型。
不是所有的矩阵都可以很容易被变成若尔当标准型,因为这需要特征值严格相等。而在数值计算中,一个值些微的变化就能导致特征值变化甚至秩的变化。所以计算若尔当标准型很不友好。
下面的矩阵也拥有特征值4和4,所以
$$
\begin{equation}
\begin{bmatrix}
5&1 \\
-1&3
\end{bmatrix}
\end{equation}
$$
下面的矩阵的四个特征向量都是0,秩为2,有两个线性无关的特征向量。
$$
\begin{equation}
\begin{bmatrix}
0&1&0&0 \\
0&0&1&0 \\
0&0&0&0 \\
0&0&0&0
\end{bmatrix}
\end{equation}
$$
下面的矩阵也一样
$$
\begin{equation}
\begin{bmatrix}
0&1&0&0 \\
0&0&0&0 \\
0&0&0&1 \\
0&0&0&0
\end{bmatrix}
\end{equation}
$$
但这两个矩阵不是相似矩阵,从它们有不同的若尔当块可以看出。
若尔当块如下,主对角线上是重特征值 $\lambda_i$,上方对角线都是1,其他位置的元素都是0。每个若尔当块只有一个特征向量,多个若尔当块可以拼成一个若尔当矩阵。
教授说,第一个矩阵上面 3x3 是一个若尔当块,下面 1x1 是一个若尔当块。我不是很明白,因为上面 3x3 不是有两个特征向量么?其实我搞错了,特征向量对应的是 $ A - \lambda I$ 的零空间而不是列空间。
若尔当的理论是,每个方阵 A 和某个若尔当矩阵 J 相似。而这个若尔当矩阵中的块的数量是特征向量的数量。
而对于比较好的情况,也就是有不同的特征值,那么若尔当矩阵就是对角阵 $\Lambda$。也就是说若尔当块只是比对角矩阵多了对角线上方的一些1,这已经是最优的了。
这里补充下几何重数和代数重数。
代数重数:也就是矩阵特征多项式中,某个解也就是特征值的重数。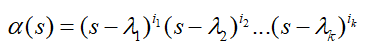
几何重数:矩阵某个特征值对应的特征空间的维度。也就是 $A-\lambda I$ 的零空间的维度。
L30 奇异值分解(SVD)
这是线性代数的核心部分。是矩阵最终和最好的分解。
一个矩阵会被分解为一个正交矩阵 $U$,一个对角矩阵 $\Sigma$ 和一个正交矩阵 $V$ 的乘积。即 $A = U \Sigma V^T$。
首先介绍两个特殊情况:
- A 是正定矩阵,那么 A 可以被分解为 $Q A Q^T$
在第 L26 课中讲过,实对称矩阵的特征向量是正交的。 - A 可对角化,那么 A 可以被分解为 $ S A S^{-1}$
但需要注意,这里的正交向量矩阵 S 未必是正交的。
如何做到呢?我们可以在行空间找某个 $v_1$,它变换到列空间里是 $ u_1 = A v_1$。在奇异值分解中,找的是行空间里面的一组正交基,变换到列空间里面的一组正交基上。
此外,零空间上的向量对应了对角矩阵对角线上为0的元素。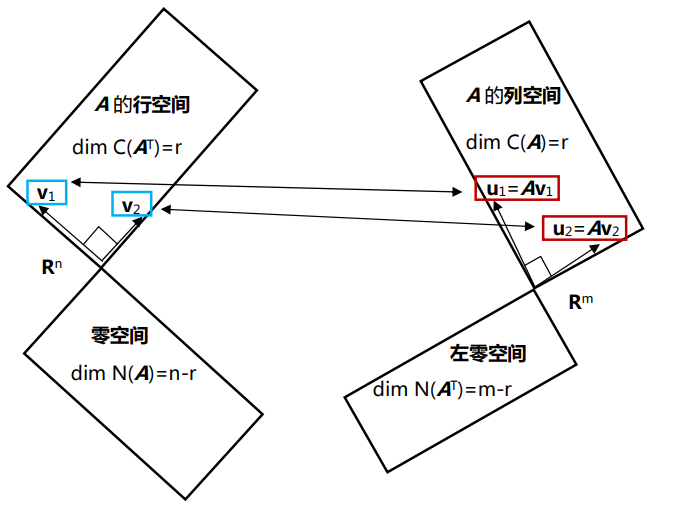
首先,通过施密特正交化,可以将行空间的一组基转化为一组正交基。但并不是所有的正交基在变换后都还是正交的,所以要找特殊的一组正交基。
这里的 r 表示矩阵的秩。如果加上零空间的部分,则有 $A V = U \Sigma$。其中零空间对应的正交基是 $v_{r+1} , …, v_n$。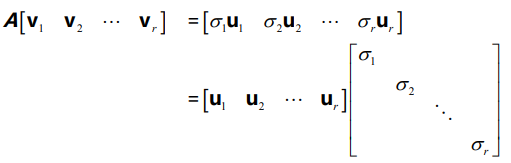
Reference
- https://zhuanlan.zhihu.com/p/470026382
几何重数和代数重数

