语法分析实战

1959年，Chomsky证明了文法和自动机的等价性，由此形式语言诞生了。目前，我们主要探讨4类文法，正则文法（确定有限自动机或非确定有限自动机）、上下文无关文法（下推自动机），上下文有关文法（线性有界自动机）、无限制文法（图灵机）。
有限自动机具有有限种状态。
上下文无关文法(CFG, Context Free Grammar)属于二类文法，其能力等价于下推自动机(PDA)。相对于三类文法即正则文法，上下文无关文法能够对非终结符做状态转移。
图灵机的状态也是有限的。图灵机的“内存”不是栈，而是纸带，由此可以看做是有两个栈的PDA。
自上而下和自下而上是两种常用的上下文无关文法分析方法。
自上而下的方法的难点在于选择哪个产生式进行推导，自下而上的分析方法难点在于在不同的格局下选择移进或归约的矛盾。

本文定义和基础概念

1. 文法G[S]
   以S为开始符号的文法

2. 拓广文法G'[S']
   LR分析中用到的。
   如果文法G的开始符号是S，则G的拓广文法G’是在G的基础上增加一个开始符号S’，和产生式S' -> S。其目的是保证开始符号始终在左部，从而当它被归约时，说明整个语法分析过程结束并成功。

3. 文法符号
   可以是终结符，也可以是非终结符

4. 符号串
   文法符号的串，所以可以是终结符，可以是非终结符

5. ε规则

6. #或者$
   表示EOF

7. V
   表示文法的符号表，包含终结符和非终结符。

8. V*，即Kleene星号运算/Kleene闭包
   称为V的闭包。
   表示V上所有有穷长串的集合。

   {'a', 'b', 'c'}* = {ε, "a", "b", "c", "aa", "ab", "ac", "ba", "bb", "bc", ...}

9. 大写英文字母，如A、B、C
   表示非终结符

10. 小写英文字母，如a、b、c
    表示终结符

11. 希腊字母，如α、β、γ
    表示符号串，由若干(可以为0)个文法符号(终结符和非终结符)构成。

12. 箭头->
    表示产生式。产生式一般为α -> β，其中α必须包含一个非终结符。

13. 箭头=>
    表示1步推导。
    其中=>+表示经过大于等于1步的推导；=>*表示经过大于等于0步推导。
    =>R表示最右推导，其实也就是规范推导。
    =>*R就是上面的结合了。

14. 箭头<=
    表示归约

15. 句型(sentencial form)α
    推导过程中生成的产生式。
    句型可以包含终结符或者非终结符，也可以是空串。例如在S->A->aB->ab中，A、aB、ab都是句型。

16. 规范句型/右句型
    最右推导得到的句型

17. 句子(sentence)
    不包含非终结符的句型

18. 推导
    从开始符号推导出和输入串相匹配的句子。

19. 归约
    用非终结符代替一段文法符号串，这是和推导的相反过程。
    通常需要解决两个问题，一是何时进行归约(可能导致移进-归约冲突)，二是使用哪一个产生式进行归约(可能导致归约-归约冲突)。

20. 最右推导(rightmose derivation)和最左归约
    最右推导称为规范推导，指每次选择句型最右边的非终结符进行推导。
    最左归约称为规范归约，表示自左向右的归约过程。指每次对最左简单短语进行的归约。

21. 移动归约语法分析器

短语、直接短语和句柄，这三个概念的范围是依次缩小的。下面关于它们的定义，被用在《自下而上的分析方法》这一章节中，但我们提上来讲一下。

1. 短语
   短语指的是一个符号串，一个句型的语法树中任一子树叶节点所组成的符号串γ都是该句型的短语。我们称γ为这个句型相对于A的短语，其中A为该子树对应的非终结符。
   形式化地，对于文法G的起始符号S，如果满足下面两个条件，则β是句型αβδ相对于非终结符A的短语。

   S =>* αAδ
   A =>+ β

   简而言之就是说，从开始符号S能够推到包含非终结符A的句型，并且这个句型中的A能够被推导到符号串β，那么符号串β就是相对于非终结符A的短语。粗略可以理解为，A在文法里面真正能推导出来的符号串β，就是A的短语。

2. 直接短语
   直接短语更进一步，要求选择的子树不应该含有其他子树。实际上就是它的孩子全部都是叶子。对于A，应用产生式A -> β得到的β，β的所有符号对应到树中都是叶子节点。
   形式化地，如果满足A => β，则β是句型αβδ相对于规则A -> β的直接短语。容易看到，这里相对短语的唯一限制是，改为了1步推导=>。结合下面例子中的图可以看出，T*F是直接短语，E+T*F只是短语，原因是T => T*F，但E =>+ E+T*F。
   值得注意的是这并不意味着这些叶子都是终结符。

3. 句柄(handle)
   句柄是最左直接短语。即，如果有推导S =>* αAw ->* αβw，则紧跟在α后面的产生式A -> β，是αβw的句柄。我们可以用这个句柄，将β归约成A。可以省略产生式，简洁说β是αβw的句柄。这里强调w是终结符串，原因很简单，我们是最左归约，你右边哪里整出来的非终结符？
   简单来说，一个符号串的句柄是和产生式右部匹配的子串，并且最左归约要求将它归约到该产生式左边的非终结符。但这是一个很宽泛的条件，并不是所有A -> β的β都是句柄，因为β不能被归约成A，因为可能A不能在随后被归约成开始符号S(后面会给出一个aAAcde的例子)。
   句柄又被称为“可归约串”，这是因为自下而上的分析方法总是等到句柄出现后进行归约。如果句柄还没出现，那么已有的部分就是活前缀。
   语法分析器在读取输入串的每一个符号时要选择对这个符号是移进还是归约、按那个产生式归约，实际上LR0、SLR1、LR1、LALR1文法的差别体现于此。但无论如何先要找到句柄。
   如果语法是有二义性的，那么句柄可能不唯一，因为可能有不止一个αβw的最右推导。

4. 活前缀(viable prefixes)
   出现在移动归约语法分析器栈中的右句型前缀的集合称为活前缀。反过来讲，活前缀是右句型的前缀，并且右端不会超过该句型最右边句柄的末端。
   简单理解，活前缀就是句柄的子集，状态机移进的过程就是在分析活前缀，在发现一个句柄之后就立马归约这个句柄。

举出下面的例子

E -> T | E + T
T -> F | T * F
F -> (E) | i

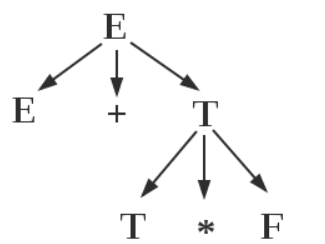
研究下列句子，此处i1/i2/i3其实都是i，后缀是用来标识具体是哪一个i，方便讨论。

i1 * i2 + i3

容易看出

1. i1是这个句型相对于非终结符F的短语。

   E =>* F * i2 + i3
   F => i

   进一步地，因为F => i是一步，所以i1同时也是F -> i规则的直接短语。
   进一步地，i1是最左直接短语，也就是句柄

2. 对于i2、i3，也能得到类似的结论，但它们不是句柄。

3. i1是这个句型相对于非终结符T的短语。
   这是因为

   E =>* E + i3 => T * F + i3 =>* T * i2 + i3
   T => F => i

   但是因为

   T =>+ i

   所以不是直接短语

4. i2 + i3不是这个句型的短语。
   这是因为，虽然有

   E =>+ i2 + i3

   但是没有下面的推导

   E => i1 * E

文法和自动机

正则文法

产生式具有下面格式的是正则文法：

A -> a
A -> aB
C -> ε

可以发现，正则文法中的产生式必须是以终结符开头，或者是个ε规则。
解析正则文法可以通过DFA，整个过程不会涉及递归。

DFA和NFA

可以通过子集法将NFA转化为DFA。
方法分为2步：

1. 找到ε-closure
   从开始节点开始，对于NFA中的每一个节点，找到它能通过ε规则到达的所有节点。
   这是一个递归的过程。
2. 把这些closure作为新的DFA节点

可以参考Leetcode 10。

上下文无关文法

产生式具有下面格式的是上下文无关文法：

A -> α

容易看出，上下文无关文法要求产生式左边是一个非终结符，右边是符号串。

上下文无关文法取名为“上下文无关”的原因就是因为字符 A 总可以被字符串 α 自由替换，而无需考虑字符 A 出现的上下文。

demo

C不是上下文无关语言。我们可以举出反例：因为C要求标识符的声明先于引用，并且允许标识符任意长。因此，描述C的文法只是用id这样的记号来代表所有的标识符，在编译C时，语义分析阶段需要检查标识符的声明必须先于引用。

同样VB和Fortran也不是上下文无关语言，因为A(i)可能是数组或者函数，这同样需要语义分析程序进行处理。在我的CFortranTranslator中，在语法分析阶段把数组的slice和dimension部分看作一种特殊形式的参数表进行处理，从而实现和函数的同意。事实上，很多需要用更强的文法分析方法的问题可以在语义阶段较轻松地解决。

上下文无关文法和下推自动机的等价性

1. 证明如果一个语言是上下文无关语言，那么我们能够构造一个NPDA对语言中的任何符号串产生一个最左推导。

上下文有关文法

上下文有关文法允许产生式的左边同时有终结符和非终结符(这也就是所谓的上下文)，例如

αAβ -> αγβ

自上而下的分析方法

自顶向下分析方法相对来说比较符合人的思维，比如我们交谈时一个句子听到一点中能估计到大概的意思，而不是要把一句话听完才能恍然大悟。正因为如此，编译器写起来也方便，因为符合人的基本思维。

自上而下的分析方法分为非确定的和确定的两种，确定指的是根据当前的输入符号，选择用来推导产生式是唯一确定的；对应的，非确定的自顶向下分析可以在关于一个非终结符有多个候选产生式的时候进行回溯，也就是说一个不行，我们就再试下一个，这里面通常还有递归在里面，所以效率较低。

确定的分析方法对文法要求较高，例如文法中就不能出现左递归和左公因子。

递归下降法

确定的LL(1)预测分析法

LL分析(以下出现的LL分析指代LL(1)分析)，是一种确定的自顶向下分析技术，确定体现在在推导过程中可以完全按照当前的输入符号(或者再向前看k-1个符号)决定哪个产生式向下推导。
一般手写LL分析是很方便的，这是因为在语法分析的同时可以借助于语义分析来避免潜在的语法冲突。

而LR方法并不容易在里面嵌入语义分析模块，这也很容易理解：只有在归约时，才最终确定归约到哪个非终结符。既然都已经决定归约成啥了，那冲突就已经解决了。

LL分析法主要是去构造三个集合。

FIRST集

FIRST集是对于一个句型α来讲的，得到一个终结符集合。FIRST集表示一个句型所有可能的第一个非终结符。注意如果α可推导为ε，则ε也属于FIRST集。可以得到所有文法符号的FIRST(X_i)集的生成方法：

1. 终结符的V_T的FIRST集是自己，这是显然的
2. 非终结符X的FIRST集包含以下内容：
   1. 包含ε
      1. 如果X有产生式X -> ε。
      2. 或者X有全部由非终结符组成的产生式X->Y1Y2...Yn，并且这些非终结符Yx全部有ε产生式Yx -> ε。
   2. 包含终结符a
      如果X有以a开头的产生式。
   3. 包含所有非终结符的FIRST集，但是要除去所有的ε
      如果X有全部由非终结符组成的产生式，并且存在一个非终结符没有ε产生式。
      例如X->Y且Y => ε，则加入FIRST(Y) - ε。
      又例如X->Y1Y2且其中Y1 => ε，但不能推出Y2 => ε，则加入(FIRST(Y1) - ε) ∪ FIRST(Y2)。这是显然的，因为X->Y1Y2不能推出ε，但如果写成FIRST(Y1) ∪ FIRST(Y2)，里面就包含了ε。

FOLLOW集

FOLLOW集是对于一个非终结符A来讲的。表示所有可能在A后面的终结符。在计算时，{ # }和所有A->αBβ产生始终的FIRST(β)的非空元素都属于FOLLOW(B)。当然β可能推导为空，这样的情况下也将FOLLOW(A)加入FOLLOW(B)中。然后反复直到各个FOLLOW集合不再增大。容易看出FOLLOW集的计算需要依赖FIRST集。

SELECT集

SELECT集是对于一个产生式A->α而言的，返回的是终结符的集合。当读取到终结符a时，对于A的所有产生式A->α，如果终结符在a在SELECT(A->α)集合中，那么就可以用这个产生式A->α推导。
显然，当推导出错时没有这样的产生式，否则有且仅有一个这样的产生式。
注意，SELECT(A->α)集合中可能有多个终结符。但是，同一个终结符a只会在非终结符A的一个SELECT集中，即通过键值对<A, a>可以唯一确定一个产生式。
容易发现SELECT(A->α)有两部分组成，一部分是α不推导为ε时候，是FIRST(α)，一部分是α推导为ε时候，是FOLLOW(α)。

将非确定的文法转换成确定的LL(1)文法

提取左公因子

左公因子的存在会导致SELECT集相交，这是显然的。
对于显式的左公因子，直接提出来即可，如

A -> αβ|αγ

可以变为

A -> αA'
A'-> β|γ

对于隐式的左公因子（即左边以非终结符开头的情况），可以使用关于该非终结符的所有右部以终结符开头的产生式展开，例如

A -> ad
A -> Bc
B -> aA
B -> bB

展开得到

A -> ad
A -> aAc // B => aA
A -> bBc // B => bB
B -> aA
B -> bB

消除左递归

考虑下面的文法

A -> Ab
A -> a

可以发现对于非终结符A，并不能确定用来推导的产生式，于是只能采用非确定的递归下降法，寻找最左非终结符，于是会陷入展开A的死循环A => Ab => Abb => Abbb。
通过改写文法消除左递归后，这就是一个确定的文法了

A -> aB
B -> bB
   | ε

还要注意一点，有些人会将左递归和尾调用等同起来，但这是不同的两个概念：

1. 左递归是针对文法而言的。不消除左递归，不能使用确定的自上向下分析。
2. 尾调用是对于一个函数调用而言的。当一个函数的最后一个工作是调用自己的时候，这样的调用称为尾递归，例如计算阶乘的某些实现。当这个函数计算仅占用常量的栈空间的时候，特别是对于LISP这样的函数式语言，可以进行尾递归优化(Tail Call Optimization, TCO)，即可以不在调用栈上面添加一个新的栈帧，而是更新它，如同迭代一般。通过尾递归优化，可以将$O(n)$的栈帧使用变为$O(1)$，减少部分递归程序的开销。

自下而上的分析方法

自下而上的方法可以理解为从输入串归约为开始符号S的过程，常见的有如下的一些分析方法：

1. 移动归约分析法
   不能处理移进归约冲突和归约归约冲突
2. 算符优先分析法
3. LR分析法

例如考虑文法

S -> aABe
A -> Abc | b
B -> d

则从上往下是句子abbcde归约到开始符号，而从下往上是一个最右推导，两个互为逆过程

abbcde
aAbcde (产生式1)
aAde   (产生式1)
aABe   (产生式2)
S      (产生式0)

注意，aAAcde不是句柄，因为不能被归约到S。

算符优先分析法

算符文法的特性是：

1. 所有产生式的右端都不是ε，或两个相邻的非终结符

例如下面的文法不是算符文法

E -> EAE | (E) | -E | id
A -> + | - | * | /

但可以代入A得到一个算符文法

E -> E + E | E - E | ... | id

因为减号可能是一元或者二元的，这给算符优先分析法带来了一些困难。但它常被用来处理表达式。

LR分析法

介绍LR(k)分析法，L表示从左到右扫描，R表示构造最右推导的逆过程，k表示向前看k个字符。特点：

1. 基本能识别所有使用CFG的程序语言语法结构
2. 是已知的最一般的无回溯移动归约语法分析法
3. 在从左到右扫描时，LR语法分析器能及时发现语法错误

如下图所示，LR分为几个部分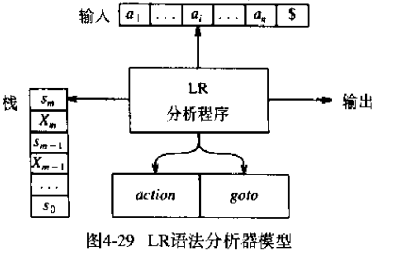

1. 分析栈(状态栈和符号栈)
2. ACTION表和GOTO表

分析栈(状态栈和符号栈)

有的书上是分开来的，龙书上是合成一个栈的，其实都无所谓。因为状态和符号是interleave的。

每个状态符号si都概括了栈中位于它下面的信息。

// 对应到上图，sn是栈顶
s0 X1 s1 X2 s2 ... Xn sn

在实际实现中，文法符号不需要出现在栈中，也就是说我们不需要符号栈。所以实际上只有一个栈，也就是说LR方法实际上对应一个下推自动机。而事实上CFG的描述能力就等价于一个下推自动机，那么LR方法用下推自动机来解析CFG是再正常不过的了。

ACTION表和GOTO表

有了状态，自然就会想到状态机。但我们这个状态机有点特殊，它是一个下推自动机。因此需要用两个表ACTION表和GOTO表来驱动下推自动机。
ACTION表和GOTO表可以被认为是两个二维数组，其中ACTION表的两个维度是状态和终结符，而GOTO表的两个维度是状态和文法符号。

ACTION[Si, a]表示状态栈顶为Si时，读入输入符号a时需要采取的Action。它在移进和归约发生时都有作用，包含：

1. 移进
   此时还在构造活前缀。
   如果有Sj = ACTION[Si, a]，则Si入状态栈，a入符号栈。
   这里清华的教材把ACTION写成了GOTO，应该是个错误。
2. 归约
   当句柄β的右端出现在符号栈顶时，将它归约成对应的非终结符A。此时需要找到句柄的左端，然后使用产生式对应的非终结符来替代。
   这个过程必须按照顺序执行下面的操作：
   1. 符号栈出栈|β|长度个文法符号，这些文法符号一定能匹配β。
   2. 符号栈压入A。
   3. 状态栈压栈，Sj = GOTO[Si, A]，表示归约后到达的状态。
      龙书上因为将符号栈和状态栈合二为一，所以是弹出2 * |β|个符号。
3. 接受acc
   符号栈只剩开始符号S，且没有剩余的输入符号。
4. 报错

GOTO[Si, a/A]表示状态栈顶为Si时，遇到文法符号(终结符a或者非终结符A)时需要转移到的状态。它只在归约发生时有作用。

因为栈顶的状态符号包含了确定句柄所需要的一切信息，所以LR分析器不需要遍历整个栈就可以知道栈顶是否是句柄的有关，在编译器实际处理过程中并不需要访问非栈顶元素。教科书中之所以画出了栈是为了方便理解。

给出文法

(1) S -> aAcBe
(2) A -> b
(3) A -> Ab
(4) B -> d

下图是该文法的一个GOTO和ACTION表。在ACTION表中，Si表示一个移进并转移到状态i；rj表示按照产生式j进行归约，对于每一个归约动作都会通过GOTO表来表示归约后到达的状态。这表中的空白都是出错状态。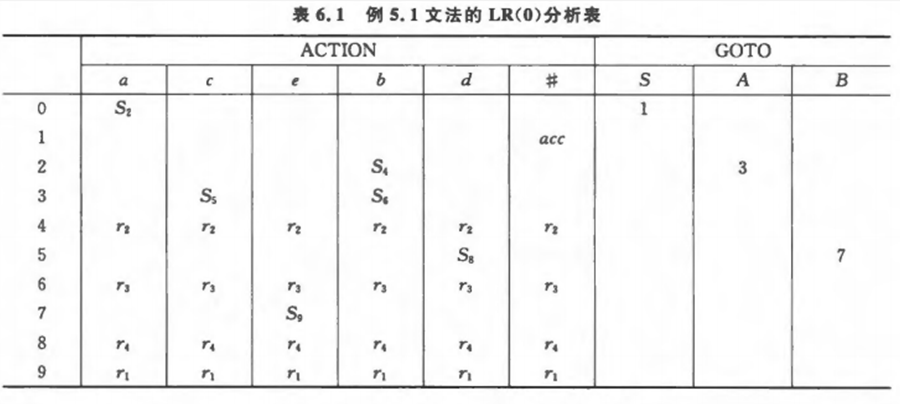

我们基于abbcde#分析，一开始状态栈为0，符号栈为#：

1. 第1步
   ACTION(0, a)，转移到状态2，这是一个移进。
2. 第2步
   ACTION(2, b)，转移到状态4，这是一个移进。
3. 第3步
   此时状态为4，读入符号还是b，查看ACTION(4, b)，发现这一行全部是r2，因此按照产生式2，即A -> b进行归约，即：
   1. 首先，要移除移进被归约的状态号和符号。此时，符号栈变为#a，状态栈变为02。
   2. 然后，得到非终结符A，压入符号栈。此时，符号栈变为#aA，状态栈不变。
   3. 然后，根据栈顶元素执行状态转移。注意到现在状态栈顶不再是4，而是2了(这也是我们之前提到为什么要按照顺序的原因)。于是我们查看GOTO[2, A]，发现值为3，进行压栈。此时状态栈变为023。
4. 第11步，我们按照产生式1进行归约操作

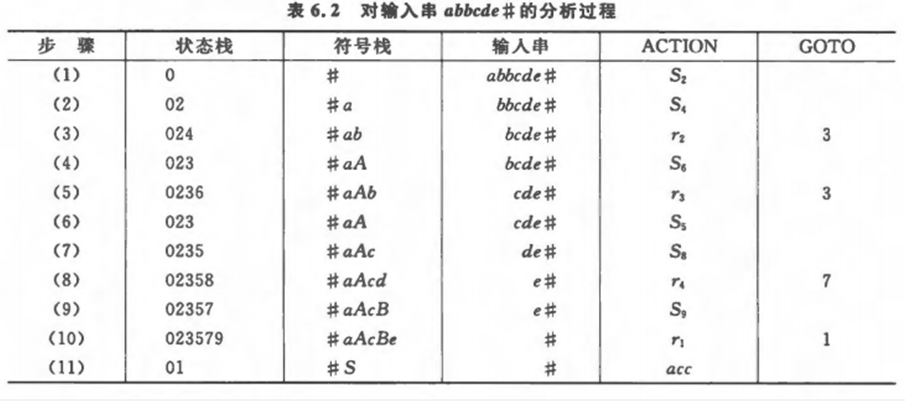
可归前缀和活前缀

步骤3/5/8/10是执行的是归约动作，此时它们符号栈中对应的符号串被称为可归前缀。

给出活前缀的形式化定义：考虑下面的文法G中的推导，这里w是终结符串，A是最右非终结符。对A进行推导，所以这是一个规范推导(最右推导)过程。其实在定义句柄的时候，我们已经见到过这样的过程了，那时我们定义了β是句型αβw相对于非终结符A的短语

S'=>* αAw =>* αβw

插一句嘴，容易看到，规范推导的一般形式如下，这也印证了规范推导是最右推导。

文法符号串(α) 待推导的非终结符(A) 终结符串(w)

如果符号串γ是αβ的前缀，那么γ是文法G的一个活前缀。同时，γ是规范句型即右句型的前缀。

活前缀的作用是什么呢？而一旦栈中出现αβ，也就是形成了A的句柄，那么就可以按照A->β归约。因此，只要输入串的已扫描部分可以归约成一个活前缀，那就意味着已经扫描的部分没有错误。这也是它为什么叫“活”的意思。其实在英文中，活前缀的活被翻译成viable，也就是说得到句柄要经由活前缀的构造，这又点出活前缀的另一层意思。

LR分析栈中的文法符号总是构成活前缀。

容易发现：

1. 可归前缀和活前缀的关系
   规范句型(最右推导得到的句型)中形成可归前缀中的所有前缀都是活前缀，可归前缀也是活前缀。活前缀是一个更大的概念。
2. 可归前缀和句柄的关系
   句柄是可归前缀的一部分(这两个不是一个东西)。句柄和可归前缀的右边是对齐的。

构造ACTION表和GOTO表的方法

有了ACTION表和GOTO表，我们就能驱动状态机了。但这个表是如何得到的呢？

主要有三种方法：

1. 求出所有活前缀的正规表达式，构造NFA，转化为DFA
2. 求出文法中所有的项目，构造NFA，转化为DFA
3. 通过CLOSURE和GO函数

LR(0)分析构造DFA的理论方法

项目

在文法G的产生式的右部的适当位置加一个点·，得到一个**项目(item)**。这个点有点类似于光标一样，可以在最左边或者最右边。

对于A -> ε，只有一个项目A -> ·

点的左边表示打算用这个产生式归约时，已经被识别的句柄部分；右边表示期待的后缀部分。

项目有下列分类，其中

1. 移进项目A -> α·aβ
   分析时将a入栈。
2. 待约项目A -> α·Bβ。
   如果圆点后面是个非终结符，表示先要把一些串归约成B，才能继续分析β
3. 归约项目A -> α·
   一个产生式的右部已经被分析完了。
4. 接受项目S' -> α·

项目、项目集、项目集规范族

LR分析表本质上等同于一个识别整个文法的活前缀和可归前缀的DFA。
考虑文法，规定S'-> ·E为初始状态，因为它是拓展文法开始符号S'的产生式(唯一的)所对应的项目。

S' -> E
E -> aA | bB
A -> cA | d
B -> cB | d

列出所有的项目如下图所示

所有产生式的每个项目都对应于NFA的一个NFA状态，得到如下NFA。

这里双圈表示识别句柄的状态，双圈加上星号表示识别句子的状态。

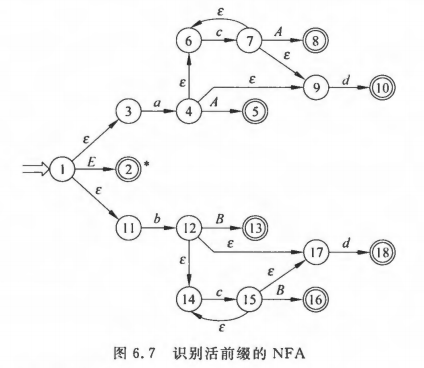
通过子集法确定化这个NFA，得到下面的DFA。DFA中的每个DFA状态现在对应一个项目集(set of items)I，也就是一组项目的集合。可以发现，不同于NFA，DFA的状态现在和项目是一对多的关系了。

下图中的I0表示DFA上0状态的项目集。我们不管DFA的节点是啥，而只根据边来走，如果能走到“叶子”，就说明得到了可以被接受的句子。【Q】在这里会产生一个疑问，对于非终结符的边，是不会走到的，它们的作用是啥呢？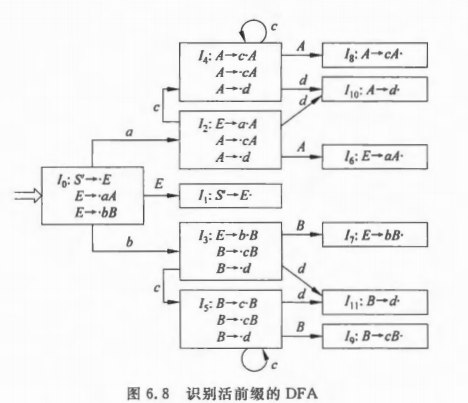

识别一个文法活前缀的DFA项目集的全体称为这个文法的项目集规范族。简单的讲，项目集规范族就是项目集的全体，它的范围和DFA是等同的。

NFA的构造过程

我们需要有确定的办法来求出所有活前缀和可归前缀，才能构造出这个NFA。为此，我们有定义6.2，其中α是符号串，ω是终结符串、S'是拓广文法的开始符号。

LC(A) = {a | S' =>*R αAω }

那么，这里的LC(A)表示规范推导中非终结符A左边出现的符号串的集合。
其实这个定义是显而易见的，我找到A出现的所有地方，然后我看看它前面可能出现哪些串就行了。容易发现，这个是可以用类似DP的方法来生成的。比如说如果我有β -> γAδ，那么对于任意的α ∈ LC(B)，一定满足

αγ ∈ LC(A)

证明很简单，我们只需要观察到

S' =>*R αBω =>R αγAδω

下面还会提到一个实用的构造方法，即“SLR”。

SLR(0)分析

这个方法也就是所谓的SLR(0)方法，核心也是构造识别活前缀的DFA。
它在遇到可以归约的句柄时，始终选择归约。

构造NFA

其实这个方法，看上面的NFA的demo就能猜个大概。
考虑出自于同一个产生式的项目i和j，如果i项目是

X -> X1 X2 ... Xi-1 · Xi ... Xn

j项目是

X -> X1 X2 ... Xi · Xi+1 ... Xn

也就是说从i到j，小圆点右移了一个文法符号，那么就从i向j连一条线，它的标记是Xi。

特别地，如果Xi是非终结符，那么也存在以它为左部的状态，例如Xi -> ·β，令它是状态k，那么我们从状态i向状态k连一条线，标记为ε规则。

构造DFA

既然已经得到一个NFA了，当然就可以使用子集法把这个NFA确定化为一个DFA，但是这样计算量很大。因此引入下面的方案。

闭包CLOSURE运算

闭包CLOSURE是针对一个状态即项目集I而言的，CLOSURE(J)表示状态J的项目集。通过闭包，可以求出DFA一个状态的项目集，其方法是

1. I属于闭包
2. 对于闭包中的所有项目，首先判断项目类型:
   1. 如果是待约项目A -> α·Bβ
      将非终结符B的所有产生式，即形如B -> γ的产生式，作为B -> ·γ加入闭包。
      这是一个递归的过程，因为被添加进去的项目，又会被拿出来计算。
   2. 如果是移进项目
      不属于当前状态对应的项目集，不需要加入闭包。
   3. 如果是归约项目
      不需要加入闭包。

引入核心项目简化存储

从CLOSURE的计算规则中可以看到，如果项目集中包含项目A，那么所有形如项目B也应该在这个状态内。

A -> α·Bβ
B -> ·γ

还是上面的例子，我们考虑NFA图中的项目1，在确定化得到状态I0后，发现除了项目1之外，还多了两个项目E -> ·aA和E -> ·bB，它们是对E求闭包得到的。

S' -> ·E
E -> aA | bB

诸如这样的项目事实上可以被省略，因为它们可以通过对核心项目求闭包得到。核心项目(kernal item)包含：

1. 初始项目
   例如S' -> E，其中S’为拓广文法G’的开始符号。
2. 圆点不在左端的项目
   例如E -> ·aA和E -> ·bB这些圆点在左端的项目，可以直接用其产生式左部的非终结符来代指，所以不算是核心项目。

通过对核心项目求闭包始终可以得到所有的非核心项目，因此在存储的时候，我们只需要存储核心项目就行了。

GO函数

转换函数GO用来求出移动圆点之后的新的项目集。龙书中将其定义为goto函数，因为容易和GOTO表混淆，所以我们采用清华的命名，也就是GO函数。但其实GO函数和GOTO表就是类似的东西，只是GO函数的第一个参数是项目集，而GOTO表的第一个参数是DFA状态。

定义GO函数如下，其中I是包含某一项目集的状态，X为终结符或非终结符。对于I中任何型如A->α·Xβ的项目，右移小圆点，得到的A->αX·β称为该项目的后继项目。那么I所有后继项目的集合就是J。

GO(I, X)=CLOSURE(J)

直观地来说，**如果状态I能够识别活前缀γ，那么状态J能识别活前缀γX**。再意会一下，GO(I, X)表示将X的小圆点右移之后，从I“派生”出来的新的项目集。

因此这里就产生一个迭代的过程了，迭代的最终结果就是求出整个项目集规范族。

求项目集规范族

通过CLOSURE和GO函数，可以求到某一个项目集，下面需要通过右移圆点的办法，得到项目集规范族。求项目集规范族的过程为：

1. 对初态S'求闭包，得到一个完整的项目集
2. 对于得到的项目集中的每个项目，读入一个文法符号X，向右移动圆点，也就是应用GO函数。读入不同的文法符号会通向不同的新状态/项目集
   注意原项目集I中的两个项目在读取同一个文法符号X之后必然属于同一个状态/项目集，即使它们对应的产生式左部不相同，这是由于GO(I, X)是唯一确定的。
3. 对于这些新状态，再求闭包，由此循环

如下图所示，对于文法4.19，从I0分别右移圆点通过E、T、F、(、id，可以得到I1-I5。

有效项目

如果存在推导

S =>* αAw =>* αβ1·β2w

则可以说项目A -> β1·β2对活前缀αβ1是有效的。我们可以具体分析β2：

1. 如果是ε，说明A -> β1是句柄，应该归约
2. 否则，说明句柄还没有完全出现在符号栈中，需要移进

当然，同一个项目可能对不同的活前缀有效。同一个活前缀也可能有多个有效项目，这就出现了冲突，我们可以通过看下一个输入符号来解决冲突(将在后面看到)。

对于一个从规范项目集族构造，以GO为转换函数的DFA，那么活前缀γ的有效项目集，是从这个DFA的初态出发，沿着γ的路径能够达到的项目的集合。

构造GOTO和ACTION表

现在我们得到了拓广文法G’的LR(0)项目集规范族，它是一个关于项目集Ii的集合。

C = { I0, I1, ..., In }

分析表(GOTO表和ACTION表)可以按以下方式构造：

1. 终结符移进
   如果项目A->α·aβ属于项目集Ik，并且GOTO(Ik, a)=Ik，当a为终结符时置ACTION(k, a)为S。这实际上就是移动j进栈。
2. 终结符归约
   如果项目A->α·属于项目集Ik，则**所有的终结符a和#置ACTION(k, a)为rj。其中j是产生式的序号，表示按照第j条产生式A->α来归约。
   注意，在龙书中会限定“a属于FOLLOW(A)”，这是因为它直接讲SLR(1)了，但清华会先讲SLR(0)，下一章讲SLR(1)。
   特别地，后面介绍的SLR(1)将在这里改进，向前看a**从而决定是否移进或如何归约。
3. 非终结符移进
   如果GO(Ik, A)=Ij，则GOTO(k, A)=j。
4. 接收状态
   如果项目S'->S·属于项目集Ik，则置ACTION(k, #)为acc，即接受。
5. 错误状态

如果存在规范推导S => δAw => δα·βw那么项目[A->α·β, a]对活前缀δα是有效的。

SLR(1)分析

通过向前看解决冲突

LR(0)文法相对于LL的预测分析法，将归约的时刻推迟到了读完句柄之后。这减少了冲突，但是因为在能归约的地方总是归约，所以仍存在冲突。
下面的文法描述了类似C语言风格的变量声明，通常为t <varname> [,<varname>]。这里省略了赋初值，同时类型标识符作为一个终结符t出现，在上文中解释过这是因为受到上下文无关文法的限制

S' -> S
S -> tD
D -> D,i
D -> i

构造文法的项目集族，容易发现会产生移进归约冲突：

S -> tD· 
D -> D,·i

也就是说当遇到int i,j这样的情况，编译器现在读到j，已经形成了S->tD的句柄，可以归约了。但是这样的归约是错误的，因为后面的,j就会被丢掉了。显然解决的办法就是再往前看一个字符，如果是,，就继续移进，如果不是就归约。当然也可以引进分号，修改文法为S->tD;避免冲突。所以得到以下方案：
设

I={
    X -> α·bβ
    A -> γ·
    B -> δ·
}

则X和A、X和B有移进归约冲突，A和B有归约归约冲突。所以向前读一个输入符号a，

1. 避免移进归约冲突：若a=b则按照产生式X移进
2. 避免归约归约冲突：如果a=FOLLOW(A)则按A归约，如果a=FOLLOW(B)则按B归约。显然FOLLOW(A)和FOLLOW(B)必须不相交(当然不能和所有的移进终结符相交)。

可以发现其实这和LL(1)的预测分析法是类似的思路。只不过LL(1)向前读的是当前非终结符的第一个终结符，但是SLR(1)读的是“下一个非终结符”的第一个终结符。
SLR(1)算法的分析表(ACTION和GOTO)的构造和LR(0)算法是相似的，不同之处在于读入终结符决定归约时，只对属于FOLLOW(A)的终结符添加ACTION表中记录。

SLR(1)的二义性

SLR(1)文法都不是二义的，但存在非二义的文法不是SLR(1)。

例如考虑下面的赋值文法(文法4.20)

S -> L = R | R
L -> *R | id
R -> L

它的LR(0)项目集规范族如下

简单说明下I2，可以计算出=∈FOLLOW(R)。现在检查I2的第一项S -> L ·= R，它导致ACTION(2,=)的操作是移动状态6入栈，也就是个移进。但它的第二项又导致ACTION(2,=)是归约R -> L，冲突产生了。

但这是不是说明文法有二义性呢？仔细琢磨，其实文法中的信息没有被完全表达出来。一个左值L完全可以出现在等号的右边，但是一个右值是不能出现在等号的左边的，如果按照R->L归约，那下一步就会推出R=L形成错误。原因是虽然=在FOLLOW(r)中，但是文法中并没有R=开头的句型。SLR(1)在前一步就以移进归约冲突报错了。

上面的问题说明SLR(1)还不够强，没有能够完全利用上下文。利用的方法很简单，我们对于I2里面的不同项，继续分类讨论嘛。

另一个demo

考虑以下的情况

S -> α·aβ
A -> α·
a ∈ FOLLOW(A)

显然按照S产生式面临输入符号a时应当移进，但是按照A产生式应当归约。这种情况的产生是因为a∈FOLLOW(A)说明存在有一种符号串Aa，但不是对于所有的符号串A后面都有a的。因为通常运气不会好到所有FOLLOW集都不会出现两个及以上数目的非终结符，于是我们惊讶前面的SLR(1)算法居然也能跑！其实并不是这样，SLR(1)要求表示移进的终结符不在表示归约的终结符集(也就是FOLLOW集)里面，对于上述文法，可以求得a∈FOLLOW(S)，但是根据S->α·aβ可以看到FOLLOW(S)和{ a }是有交集的，所以SLR(1)在前一步就以移进归约冲突报错了。

LR(1)分析

SLR(1)不能完全避免移进归约冲突。原因是FOLLOW集太过笼统，那就对每个项目单独给出后继符号，即搜索符。

对于项目集A->α·Bβ、B->·γ，如果使用生成式B->γ归约，则FIRST(β)即为搜索符。可以发现，搜索符位于被用来归约的产生式之后，即

A -> α·产生式 搜索符

搜索符对β非空的项目[A->α·β, a]是不起作用的，显然这个项目是否有效，取决于β。但对形式为[A->α·, a]的项目，它表示只有在下一个输入符号是a时，才能要求按A->α·归约。这里的a的集合肯定是FOLLOW(A)的子集，有时候是真子集，实际上可以看做是FOLLOW集的对每个项目的特化。LR(1)文法的1同时也意味着搜索符是长度是1。

如果存在规范推导S => δAw => δα·βw，项目[A->α·β, a]对活前缀γ是有效的(也就是可以被用来归约)，如果满足下面所有条件：

1. γ=δα
2. a是w的第一个符号；或者w是ε、a是$(也就是EOF)

LR(1)的CLOSURE构造

LR(1)和SLR(1)的流程大致是相同的，首先也要计算CLOSURE函数。因为LR(1)项目集多了搜索符，因此CLOSURE函数需要一些修改。

同样考虑待约项目[A->α·Bβ, a]属于CLOSURE(I)，需要判断对于G’中任意产生式B->η，能不能使用它归约B。结论是当b∈FIRST(βa)时，[B->·η, b]也在CLOSURE(I)中。这里的b有两种情况：

1. 如果β是ε
   实际上b就是a了。
2. 如果β不是ε
   b就是β推导出的第一个非终结符。

换句话说，当b∈FIRST(βa)时，才能用[B->·η, b]来归约[A->α·Bβ, a]中的B。可以看到，b不仅和A的产生式有关，还和A的搜索符有关。

所以实际操作中，我们并不是简单将B->η一股脑加进去，而是先要求出FIRST(βa)。

展开来说明，对于上面的待约项目，必然存在如下的最右推导。这个最右推导看起来很恶心，其实就是把A->αBβ“代入了”A。这里后面将w拆成了ax，原因是为了表示出a，用来计算FIRST集。

S =>* δAax =>* δαBβax

令γ = δα，简化下表示

S =>* ... => γBβax => γBby

假如βαx能推出终结符串by，那么对于每个形如B->η的产生式，存在下面的推导

S =>* γBby => γηby // 这里龙书应该写错了

于是[B->·η, b]对γ有效。

构造ACTION和GOTO表

LR(1)算法的分析表(ACTION和GOTO)的构造和LR(0)、SLR(1)算法是相似的，不同之处在于读入终结符决定归约时，只使用搜索符添加ACTION表中记录：

1. 终结符移进
   【同SLR】
   如果项目[A->α·aβ, b]属于项目集Ik，并且GOTO(Ik, a)=Ik，当a为终结符时置ACTION(k, a)为S。
2. 终结符归约
   这里不同了，不再是对于a∈FOLLOW(A)，而直接用项目中的搜索符。
   如果项目[A->α·, a]属于项目集Ik，且A不是开始符号S’，则置ACTION(k, a)为rj。其中j是产生式的序号，表示按照第j条产生式A->α来归约。
3. 非终结符移进
   【同SLR】
   如果GO(Ik, A)=Ij，则GOTO(k, A)=j。
4. 接收状态
   【同SLR】
   如果项目S'->S·属于项目集Ik，则置ACTION(k, #)为acc，即接受。
5. 错误状态

其中初态是[S' -> S, #]

下图中的算法介绍了CLOSURE、ACTION/GOTO、项目集的构造方法。

demo

考虑下面的文法，对应得到的分析表如下图所示

S' -> S
S -> CC
C -> cC | d

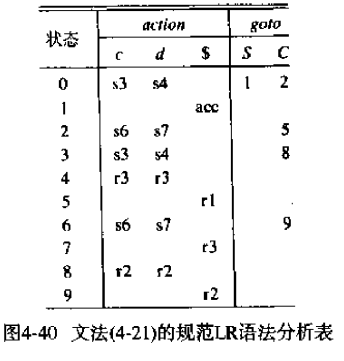
下图展示了对应的DFA，可以看到I3和I6除了搜索符是一样的，其实可以对这种进行合并，也就是LALR的思路。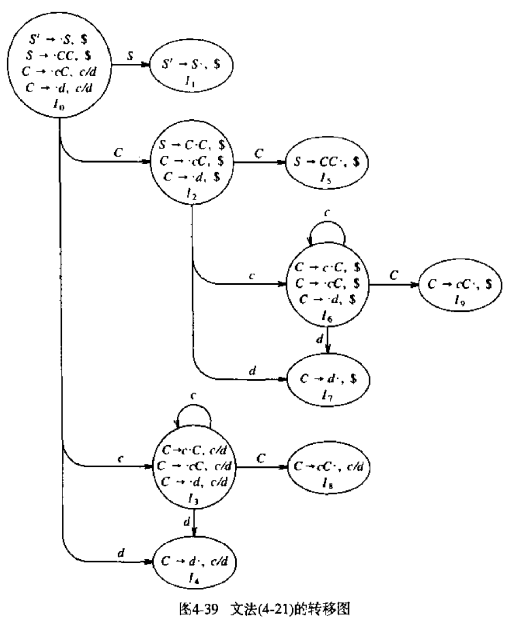

LALR(1)对LR(1)的简化

LALR的状态数是和SLR一样的，比LR要小很多。例如在解析Pascal时只有几百个状态，但用LR来处理有几千个状态。但LALR的解析能力又比SLR要强。

如果两个项目集除了搜索符其他都一样，那么它们为同心集。以上面的demo(也就是文法4.21)为例：

1. I4和I7构成同心集，心为C -> d·
2. I3和I6构成同心集，心为C -> c·C、C -> ·cC、C -> ·d
3. I8和I9构成同心集，心为C -> cC·

因为GOTO[Si, a/A]表中不依赖同心集除了心以外的成分，所以可以对GOTO表进行合并。例如，原来GOTO(I3,C)是I8，而I8现在是I89的一部分，所以GOTO(I36,C)是I89。所以在根据状态机处理时，

合并同心集后不会产生移进归约冲突。可以反证，如果出现移进归约冲突，说明对于当前的输入符号a：

1. 存在某个项目[A -> α·, a]要求按照A -> α归约
2. 存在另一个项目[B -> β·aγ, a]要求把a移进

但因为这两个项目在同心集中，说明存在某个c，使得[A -> α·, a]和[B -> β·αγ, c]出于合并前的某个集合中。而这个集合中存在有移进归约冲突了。

事实上是否产生移进归约冲突，取决于心而不是搜索符。

合并同心集后会产生新的归约归约冲突，而LR(1)则不会存在。例如下面的文法很简单，只会产生acd、bcd、ace、bce四个串，虽然c可以被归约成A或者B，但根据其前后的终结符，还是可以判断到底如何规约的，是妥妥的LR(1)文法。

S' -> S
S -> aAd | bBd | aBe | bAe
A -> c
B -> c

但考虑：

1. 对活前缀ac有效的项目集

   [A -> c·, d]
   [B -> c·, e]

2. 对活前缀bc有效的项目集

   [A -> c·, e]
   [B -> c·, d]

容易看出，当前输入符号为e可能被归约为A或B，为d也可能被归约为A或B。如果我们合并同心集，就会变成如下的归约归约冲突

[A -> c·, d/e]
[B -> c·, d/e]

这些归约归约冲突可能会导致LALR分析器不能立即识别错误。考虑处理输入串ccd，其实是不能被之前看到的4.21文法处理的。对于LR文法而言，会形成这样的分析栈。观察上面的LR分析表，会发现状态4读取$，对应一个错误

0 c 3 c 3 d 4

下面基于LALR的分析表分析。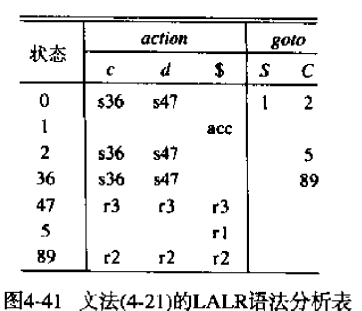

此时，我们在47状态面临$，提示可以按照C -> d归约

0 c 36 c 36 d 47

归约后得到如下，之后又可以按照C -> cC归约

0 c 36 c 36 d 89

归约后得到如下

0 c 36 C 89
0 C 2

而状态2面临$显示出错，所以在出错前，LALR会通过已有的产生式进行一些额外的归约。

构造ACTION和GOTO表(朴素)

朴素方法比较简单，很straightforward，但是耗空间。

1. 构建LR(1)文法的项目集规范族C = {I1, I2, ..., In}
2. 对于项目集中的每个心，找到所有同心项目集的并集
3. 得到C' = {J1, J2, ..., Jn}，C’是LALR(1)项目集族
4. 按照LR(1)的构建方式构建ACTION表，如果出现冲突，则说明不是LALR文法
5. 构造GOTO表
   如果某个J是某几个I的并，即这些I是同心的，那么这些I的GOTO也是同心的。不然就会产生移进归约冲突了。
   所以J的GOTO就是这些I的GOTO的并。

构造ACTION和GOTO表(高效)

首先，可以用项目集的核(也就是核心项目)来表示这个项目集。

除非α=ε，则任何调用A->α归约的项目都在该核中。考虑核项目[B->γ·Cδ, b]，有推导C =>* Aη，对于输入a，可以使用A->ε归约。其中，a∈FIRST(ηδb)。

假定存在一个LR0项目B -> γ·Cδ，其中：

1. 存在某个η，推导C =>* Aη成立
2. 进一步地，A -> Xβ是一个产生式

那么，A -> X·β应该在GOTO(I, X)中。

现在，将它扩展成LR1项目，即[B -> γ·Cδ, b]属于I，并且也扩展[A -> Xβ, a]，现在问题是哪些a能使得[A -> Xβ, a]在GOTO(I, X)中呢？

1. 如果a∈FIRST(ηδ)
   因为存在推导C =>* Aη，带入也就是B -> γ·Aηδ。实际不在乎b是啥，[A -> Xβ, a]都在GOTO(I, X)中。这是因为B的产生式中，A后面就是ηδ，而a正好属于FIRST(ηδ)。
   此时，搜索符a是自生的。例如S' -> ·S中的S就是自生的。这有点FIRST集的味道。
2. 如果ηδ =>* ε
   则[A -> Xβ, a]也在GOTO(I, X)中。现在ηδ =>* ε了，也就是A后面就没有了，B -> γ·Aηδ变成了B -> γ·A，那B的搜索符实际上就是A的搜索符，因为A是B里面的最右边的非终结符。这有点FOLLOW集的味道。
   此时，称搜索符从B -> γ·Cδ传播到A -> X·β。其中B -> γ·Cδ是I中的项目，A -> X·β是GOTO(I, X)中的项目，所以我们后面会讲搜索符从I中的项目传播到GOTO(I, X)中的核项目中去。

对于项目集I的GOTO(I, X)表中的核心项目K，下面的算法可以找出所有I中项目自生的搜索符，以及I中的会传播到GOTO(I, X)中核项目的项目。算法中的#是一个 dummy 搜索符。算法从{[S' -> ·S, #]}开始。

例如考虑下面的赋值文法(文法4.20)，首先对{[S' -> ·S, #]}求闭包如下所示。这里L的两个产生式对应的项目的搜索符还包含了=，很容易理解，因为L是左值，后面会跟一个=的，所以=是它的搜索符(还不明白可以看看搜索符的定义)。

S' -> ·S, #
S -> ·L = R, #
S -> ·R, #
L -> ·*R, #/=
L -> ·id, #/=
R -> ·L, #

项目[L -> ·*R, =]使得=是核项目L -> ·*R的自生搜索符。

下面计算LALR(1)项目集中的核心项目：

1. 首先构造LR0核心项目
2. 对于每个LR0项目集中的核心项目，以及文法符号X，应用“搜索符的自生与传播的发现”算法，确定对于核心项目而言，哪些搜索符是自生的；同时也确定从哪些I中的项目出发，搜索符可以传播到GOTO(I, X)的核项目中去
   这个过程如图“搜索符的传播”所示。
   
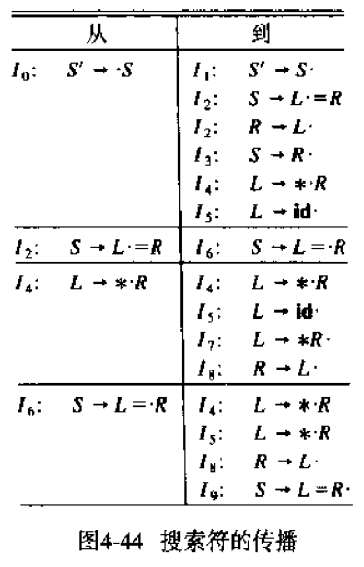
3. 对于每个项目集中的每个核心项目，列出与其相联系的搜索符。初始状态是2中的所有自生搜索符
4. 反复遍历所有集合中的核心项目，对于核心项目i，检查它能够将它的搜索符传播到哪些核心项目。这个过程在几轮迭代后会终止
   如下图所示，搜索符$由I0的S' -> ·S传播到I1-I5。以S' -> ·S传播到S -> S·为例，δ是ε，C是ε，所以η也是ε。当然这里的例子没啥代表性，因为小圆点都在最右边了，所以C一定是ε。
   搜索符=由I4的L -> *·R传播到I7中的L -> *R·和I8中的R -> L·。以前者为例，C是R，δ是ε；考虑存在的R =>* Aη，它只存在一个产生式R -> L，所以η也是ε。因此ηδ =>* ε，从而=可以从L -> *·R传播到I7中的L -> *R·。
   

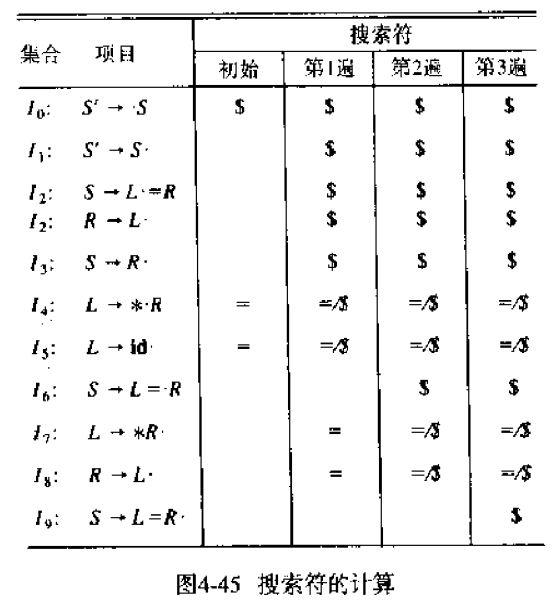
冲突的解决思想总结

我们希望文法分析过程是确定性的。也就是说：

1. 对于LL分析，希望在推导时碰到某个非终结符的产生式有多个候选的时候，能够唯一确定一个候选进行推导
2. 对于LR分析，能够唯一确定任何一时刻下的分析器的动作应该是移进还是归约(为了避免移进归约冲突)、按照哪个产生式归约(为了避免归约归约冲突)
   对于前者，例如C语言的悬空else情况if(..)if(..)else中，在else位置是移进外层的if，还是归约内层的if(实际上是选择归约)，当然这个二义文法已经不算是LR文法了。
   对于后者，例如前面所说的VB6语言A(i)可能是一个数组元素，也可能是一个函数调用，特别地，(1+2)和func_name(1+2)也可能导致归约归约冲突。

因此可以发现LR所能描述的文法是LL(1)预测分析法的真超集。回顾LL(1)预测分析法的流程，LL(1)预测分析法由一个栈S和一个预测分析表M组成。M[A,a]表示推导A时当遇到输入符a时，应当选择的A的产生式，这应当是唯一确定的。也就是说，对于任意的产生式A->α，如果a在SELECT(A->α)集合中，那就**必须要选择产生式A->α**，如果对于A的所有产生式，它们的SELECT集都不出现a，那就报错。因此，这就意味着选择A的哪一个产生式完全取决于a。

这是一个很前置的判断。例如考虑应用产生式A->lβ如下推导S=>αAbw=>rlβbw(其中α为符号串，A为最右非终结符，w为终结符串)，LL(1)预测分析法需要在看到l时就作出决定选择产生式A->lβ，但是LR分析法可以在看到b之后再决定是否把lβ归约为A，因此LR实际上获得了更多的信息。

同时LL(1)文法还是不能够出现左公因子和左递归的：对于前者可以发现同一个非终结符的所有SELECT集合是存在交集的；对于第二种情况，直接左递归A->Aβ或者间接左递归可以推出它们的SELECT集也是相交的。

有的时候，虽然文法是二义性的，但是语言却可以不是二义性的，这可以通过语义分析解决。

通过重写文法解决二义性

考虑经典的dangling else问题

stmt: if expr then stmt else stmt
    | if expr then stmt
    | other

在符号栈中出现if expr then stmt时，我们无法判断它究竟是不是句柄，因为这里出现移进归约冲突。此时输入串读到else，也许应该直接归约成stmt，也许应该继续移进找到else后面的某个stmt，再归约。这样的文法不是LR(k)文法。

可以提取公因子，重写为：

stmt: if expr then stmt optional_else
    | other
optional_else: else stmt
    | other

一般来说，对于文法

A -> αη
B -> βη

提供一个将η归约为非终结符C的产生式

A -> αC
B -> βC
C -> η

但是这样的坏处是会引入终结符C，并且这个C可能没有明确的语义作用。

通过设置终结符优先级解决二义性

这种方法常用来解决移进归约冲突

考虑通常的表达式文法：

E -> E + E | E * E | (E) | id

虽然可以通过重写文法来消除二义性。这种做法就是让高优先级的运算量(如F)经过一层归约才能变成低优先级表达式的运算量(如T)，有点类似于C++宏的那一层意思。才能但这样产生式的右边会出现单非终结符的产生式，增加了归约的次数。

E -> E+T | T
T -> T*F | F
F -> (E) | id

下面考虑优先级：

1. 对于1 + 2 * 3，能产生两种语法树，产生移进归约冲突，原因在于面临+的时候可以按照E -> E + E归约，也可以按照E-> E * E移进。于是规定*的优先级高于+。对于项目id + id · * id，向前看到*，有更高的优先级，所以选择移进。
2. 对于1 + 2 + 3，同样能产生移进归约冲突，因此规定+是左结合的，因此对于项目id + id · + id，应当归约，而不是移进。

在yacc中，支持对这些运算符指定优先级，从而既不会产生冲突，也不会要引入很多非终结符。

通过设置产生式优先级解决二义性

考虑排版文法：

(1) E -> E ^ E _ E
(2) E -> E ^ E
(3) E -> E _ E
(4) E -> {E}
(5) E -> c

其中^表示上标，_表示下标。在这个文法中并没有通过引入额外的非终结符，或者设置终结符优先级的方式，指定两个操作的优先级。

从定义形式语言的角度来讲，1产生式是多余规则，因为用2和3产生式能够得到1产生式可推导出的句子。但是从语义的角度来说它作为一个优先归约的特殊规则存在。例如以下三个排版它们的效果(语义)是不一样的

a_i² a²_i a_i²

因此单独将第一个产生式列出来，称为特例产生式，优先级最高，当满足第一个产生式时，不使用后两个产生式进行归约。

同样的方法可以用在处理A(args)和(exp)的冲突上面。这种方法常被用来解决归约归约冲突。

flex和bison是否能处理这种特例产生式呢？简单做了个demo，发现产生很多冲突。

%{
#include <cstdio>
#include <string>
#include <sstream>

#define YYDEBUG 1
#define YYERROR_VERBOSE
#define YYINITDEPTH 2000
%}

%debug
%start S

%%
S : E
E : E '^' E '_' E
    | E '^' E
    | E '_' E
    | 'c'
%%

使用GLR文法解决二义性

有时候冲突是无法避免的，这时候可以选择使用GLR文法分析器，相对于LALR分析，GLR会BFS所有可能的操作。GLR的最坏时间复杂度是O(n³)的，具体取决于冲突的数量。

通过语义分析解决二义性

例如解决Fortran过程调用和数组访问的问题。
我们构造下面的文法

stmt -> id(param_list)
param_list -> param_list , param
param_list -> param
param -> id
expr -> id
expr -> id(expr_list)
expr_list -> expr_list, expr
expr_list -> expr

在处理id(id,id)时，会遇到归约归约冲突。核心原因是无法确定将id归约成expr还是param。
一种方案是我们将param_list和expr_list合二为一。
另一种方案则是我们在词法分析时引入符号表，对于函数调用，我们将id变为procid，对于数组，我们将id变为indexid。

语义分析上的两种分析方法

语法树

语法树（推导树）的特点是非叶子节点都是非终结符，叶子节点都是终结符。因此从左到右遍历（也就是DFS）语法树即可生成代码。特别地，单趟编译器（one-pass compiler）不先建立语法树后编译。这样的编译器由语法分析带动整个编译流程，在语法分析的同时计算属性值，这样的做法称为语法指导翻译。TCC(Tiny C Compiler)就是这样的一个编译器。属性文法对遵循语法制导语义(syntax-directed semantic)原理的语言最有用，它表明程序的语义内容与它的语法密切相关。

综合属性和继承属性

考虑一棵语法树，综合属性总是自下而上传递的，例如2.4+3*4，在语法树的根节点+，得到了结果14.4，注意到类型从int上升到double体现了自下而上的过程。继承属性是在语法树水平或者从上往下传递的，例如C语言中的变量初始化语句int i = 0, j = 0;，容易得到属性文法：

T -> int| real      T.type = int| real
L -> L1, id| id     L1.in = L.in; do_symbol_table;
D -> TL             L.in = T.type

可以发现，属性先从T横向向右传递给L，然后由L向下传给L1。在产生式上来看，综合属性属于产生式的左部非终结符，从产生式右部的文法符号的属性得到（自下而上），继承属性属于产生式右部的文法符号，从产生式左部（自上而下）或者产生式右部该文法符号之前的文法符号（横向）的属性得到。

L属性文法的自顶向下和自下而上分析

自顶而下的L属性文法会导致翻译模式，也就是需要在产生式的右部文法符号中间嵌入语义计算动作(yacc中使用花括号{}括起来，里面可以写C++的代码，详情可以参考我的另一篇文章：flex和bison使用)。
考虑常见的if..elseif..else..endif文法。

if_stmt : YY_IF exp YY_THEN stmt endif_stmt
    | YY_IF exp YY_THEN stmt else_stmt
    | YY_IF exp YY_THEN stmt elseif_stmt
elseif_stmt : YY_ELSE YY_IF exp YY_THEN stmt
    | YY_ELSE YY_IF exp YY_THEN stmt elseif_stmt
    | YY_ELSE YY_IF exp YY_THEN stmt endif_stmt
else_stmt : YY_ELSE stmt endif_stmt
endif_stmt : YY_END YY_IF

PEG文法

修订

1. 表示所有可能在A后面的非终结符
   错，应该是终结符
2. 增加文法和自动机相关
   以《形式语言与自动机导论》为主体
3. 整理基本定义到单独一节

参考

1. 清华大学 编译原理
2. 龙书
3. 编译原理 中科大