B树的设计目的是减少磁盘存取，而不是诸如BST、RBT、AVL一样试图减少比较次数。根据局部性原理，当一个数据被访问时，那么它附近的数据很大概率会马上被访问，因此我们可以一同将其加载。这个原理常常被用在存取速度不同的两个设备间，如寄存器与主存（多级缓存）以及数据库系统中出现的磁盘与内存的情况。B树相对于一般的平衡BST的特点是高度低、出度大、节点大。一个高度低的树能有效减少检索磁盘的次数。一个具有较大的分支因子的树可以减少$k*log(n)$的常数$k$，其中$n$是总关键字数，也能减少磁盘存取。特别地，B树的节点设计不仅要考虑到容纳尽可能多的节点，也要同时考虑到从磁盘加载的便利性。

B树

B树具有一个最小度数$t$，表示一个节点的最小出度，我们要求最小出度必须$t \ge 2$，容易发现当$t = 1$时这个B树实际上就退化为二叉树了。B树主要构造如下：

对节点$x$
每个节点$x$应当具有$x.n$个按照非降序排列的关键字$x.key_i$。对于叶子节点$s$，它们具有相同的层高$h$。对于内部节点$x$，还具有$n + 1$个指向子节点的指针$x.c_i$。B树递归的有序性表现在对于任意一个子树$x.c_i$记录的关键字$k_i$，它满足$k_1 \le x.key_1 \le k_2 \le x.key_2 \le … \le x.key_{x.n} \le k_{x.n+1}$。如下图所示
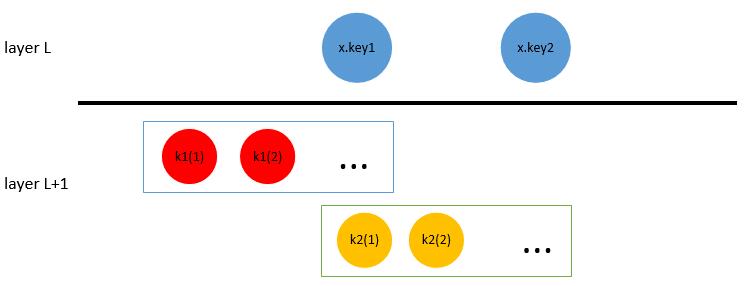
对关键字个数$x.n$
B树要求每个节点的出度在$[t, 2t]$之间，因此$x.n$的的上下界为$[t - 1, 2 t - 1]$。当一个节点中存在$2 t - 1$个关键字后，这个节点就是满的。