csapp data lab

发表于 |

csapp中的lab非常出名，在这篇文章中我主要记载第一部分，也就是data lab的解法。所有lab的源码在我的Github上。在知乎的一篇文章中记录了一些和二进制处理相关的内容，我觉得也是非常好的学习材料

abs

使用位运算求绝对值。这里用到一些位运算的基础概念。相反数的求法是~x + 1。符号位的判断方法是x >> 31，如果是负数得到的是0xffffffff（注意是算数右移），如果是正数得到的是0x0。于是可以得到下面的方法

1
2
int sgn_bit = x >> 31; 
int abs_val = (x ^ sgn_bit) - sgn_bit;

这里x ^ y是个有趣的用法，根据异或的性质，当y全为0时，返回x；而当y全为1时，返回~x。所以x ^ sgn_bit会对负数的所有位取反，而不修改正数的任何位。
不过有意思的是我这份对拍代码在Dev-C++ 5.5.3、Window10 1709版上会报Trojan:Win32/Fuerboos.C!cl。点此查看图片

logicalShift

借助右移可以在右边添加若干0，借助算数左移0x80000000可以在左边添加若干1。

1
2
int mask1 = ((1 << 31) >> n) << 1;
int mask = ~mask1;

在上面的代码中mask1这样写是为了在没有-的情况下实现1 << (32 - n)，不过这样写是不太靠谱的，在下面的fitsBits中类似的写法会导致n == 32时溢出。

bit count

这道题要求仅使用位运算! ~ & ^ | + << >>和小于0xff的数在40步之内来统计一个int32_t里面的1的数量，这题标准实现就是种群计数。
种群计数实际上是按bit的分治法，核心思想是一个$n$位数中1的数量等于高$\frac{n}{2}$位和低$\frac{n}{2}$位的1的数量的和。考虑递归的最下层需要计算一个2位数$x$，即(x & 0b01) + ((x >> 1) & 0b01)，扩展到16个2位数就成了(x & 0x55555555) + ((x>>1) & 0x55555555)，这个结果的每两位上的值表示这两位中1的数量。下面考虑把相邻的两个2位数拼成一个四位数，方法是(x & 0b11) + ((x >> 2) & 0b11)，理解也非常简单，把每个2位数当成四进制数就好。

1
2
3
4
5
6
7
8
9
int bitCount(int x)
{
  x = (x & 0x55555555) + ((x>>1) & 0x55555555);
  x = (x & 0x33333333) + ((x>>2) & 0x33333333);
  x = (x & 0x0f0f0f0f) + ((x>>4) & 0x0f0f0f0f);
  x = (x & 0x00ff00ff) + ((x>>8) & 0x00ff00ff);
  x = (x & 0x0000ffff) + ((x>>16) & 0x0000ffff);
  return x;
}

bang

这道题当时让我感到困难的地方是怎么将所有的非零值映射到一个数上。后来在网上看到解法是(~x + 1) | x，这样可以确保符号位肯定是1。

fitsBits

直观地看，一个$n$位数的前32 - n位要么全是0，要么全是1。所以可以得到下面的代码

1
2
3
4
5
6
7
8
int mask = (1 << 31) >> (32 + ~n + 1);
if (x < 0)
{
  return (x | ~mask) == 0xffffffff;
  // return (~x & mask) == 0; // de morgan
}else{
  return (x & mask) == 0;
}

下面应用下德摩根律，就可以把这个if结构缩成!((x ^ p) & mask)。

divpwr2

这道题一开始的思路是

1
return (x < 0) ? -((-x) >> n) : x >> n;

但是这样的方法是不对的，考虑当x取0x80000000时，-x就溢出了。正确方法可以借助于前面abs的求法

1
2
3
int mask = x >> 31;
int offset = ((1 << n) - 1) & mask;
return (x + offset) >> n;

注意这个offset来自于CSAPP上的公式$\lfloor x / y \rfloor = \lceil x / y + (y - 1) / y \rceil$

isPositive

这道题很简单，借此总结一下一些常用的操作。

  1. 构造0xffffffff：~0
  2. 映射0到0，非0到1：!!x
  3. 映射0到0，1到0xffffffff：~(x - 1)

isLessOrEqual

首先熟记此图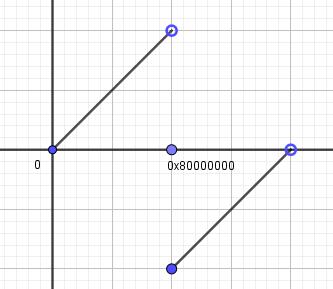

然后发现，两数同号时比较除符号位剩下的31位，否则比较符号位。因此可以得到这样的代码

1
2
3
4
5
6
7
8
9
10
11
12
int isLessOrEqual(int x, int y) {
  int sgn_x = x >> 31;
  int sgn_y = y >> 31;
  int do_cmp = ~(sgn_x ^ sgn_y); // 判断是否同号
  int cmp_res = y - 1;
  int sgn_res = cmp_res >> 31;
  if(do_cmp){
    return sgn_res == 0;
  }else{
    return !!sgn_x;
  }
}

可以按照下面的方法去掉if块

1
2
3
// do_cmp is either 0x0 or 0xffffffff
return do_cmp ? x : y;
return (do_cmp & x) | (~do_cmp & y);

ilog2

这个就是二分法，在字长小于等于4后，可以直接暴力算。注意最后结果要减1。

float_neg

从这里开始的三条是浮点数的题目。本题很简单，特判下NaN即可。注意符号位连上阶码为9位而不是8位，这真的很丑啊。

float_i2f

考虑x的绝对值ux。规格化的浮点数尾数共有24位有效数字，其中整数部分恒为1，但不显式表示出来，小数部分为23位。如果ux的有效数字不够24，那么需要左移使得其最高的1对其到24，如果有效数字超过24就需要右移，这时候发生舍入造成精度损失。阶码E是可以根据ux的有效数字算出来的，与ux需要左移/右移多少没有关系，我们应当参照小数部分的最高位，即$2^{-1}$而不是最低位$2^{-24}$，简单地来理解，由于最高位已经对齐到了整数位的个位，所以要将最高位1后面的部分也移到最高位1的后面，也就是要去掉最高位1前面的前导0。不过我很快遇到一个巨大的困难，对于0x80000001来说计算的值是0xcf000000，等于0x80000000，容易发现这里出现了一个舍入。CSAPP中说明了向偶数舍入的规则，但我不是很懂，这里看了CSDN的一篇文章终于搞明白了。其实这个说的是一个特殊情况。一般当多余数字严格小于或大于最低有效位的一半时，我们按照传统的四舍五入的规则。考虑对下面的数字舍入到小数点后3位，1.0011001 -> 1.010，这里由于1001 > 1000因此进位，同理，1.0010111 -> 1.001就直接抹掉后面四位。当多余数字刚好等于1000时，这里就应当使用向偶数舍入的原则。
最后未压缩的代码是这样的

float_twice

这个主意分情况讨论，首先NaN/无穷大还是NaN/无穷大。接着是非规格化的情况，如果尾数最高位不为1，直接<<=尾数部分，否则阶码加1切回规格化。对于规格化情况，首先增加阶码，如果阶码满了，就<<=尾数部分，并牺牲精度，容易发现随着移动自然而然能够达到无穷大（尾数为0）的情况，这体现了浮点数设计的巧妙之处。