本文从MIT的线代教程的角度重新学习线性代数。

这是第一部分，从 L01 到 L13。

前置定义

线性组合(Linear combination)是线性代数中具有如下形式的表达式。其中$v_i$为任意类型的项，$a_{i}$为标量。这些标量称为线性组合的系数或权。
$$
w=a_{1}v_{1}+a_{2}v_{2}+a_{3}v_{3}+\cdots +a_{n}v_{n}
$$

L01 方程组的几何解释

以下面的方程进行讨论
$$
\begin{equation}
\begin{bmatrix}
2 & -1 \\
-1 & 2 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
\end{bmatrix}
=
\begin{bmatrix}
0 \\
3 \\
\end{bmatrix}
\end{equation}
$$
首先可以从行向量的角度来看待，它是平面内两条线的交点。
同时还可以从列向量的角度来看待，如何对两个列向量进行线性组合，从而得到右边的向量。
$$
\begin{equation}
x
\begin{bmatrix}
2 \\
-1 \\
\end{bmatrix}
+
y
\begin{bmatrix}
-1 \\
2 \\
\end{bmatrix}
=
\begin{bmatrix}
0 \\
3 \\
\end{bmatrix}
\end{equation}
$$

考察方程$Ax=b$，对于任意的 b 它是否有解，等价于所有列的线性组合能否填满整个空间。

L02 矩阵消元

考虑下面的方程
$$
\begin{equation}
\begin{bmatrix}
1&2&1 \\
3&8&1 \\
0&4&1 \\
\end{bmatrix}
x
=
\begin{bmatrix}
2 \\
12 \\
2 \\
\end{bmatrix}
\end{equation}
$$

首先消元，做成上三角矩阵$U$。方法就是首先选定first pivot主元，位于第一行第一列的1，第一步要通过消元将第一列中除了主元之外的数字均变化为 0。操作方法就是用之后的每一行减去第一行的适当倍数。所以操作完之后，矩阵变成

$$
\begin{bmatrix}
1 & … \\
0 & …\\
0 & …\\
\end{bmatrix}
$$

然后，对第二列做类似的操作。可以看出，我们是对列求各个主元的。做完之后，会得到一个上三角矩阵。

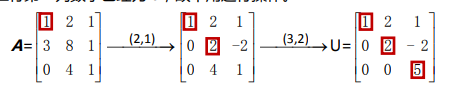
这里注意几点：

如果主元是0，就换行，也就是要主元在对角线上。
如果通过换行不能得到三个主元，那么这个矩阵就是坏的。
这里的坏，指的是不可逆。比如类似
$$
\begin{bmatrix}
*&*&* \\
0&*&* \\
0&0&0 \\
\end{bmatrix}
$$
如果找不到1作为主元，也可以通过做上面的减法得到1，不过其实主元列是不是1并不重要。因为始终可以通过某行乘以某非零常数进行初等变换。

特别地，行列式是所有主元元素的乘积，不过这个我听课的时候没听到。

下面通过增广矩阵(augment matrix)，将 $Ax=b$ 变成 $Ux=c$。

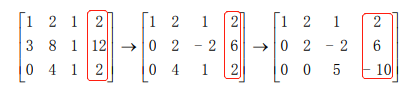
然后是回代，先算出 z，再回带算出 y 和 x。

定义$E_{21}$表示能够对位置(2, 1)进行消元的矩阵，它应该是如下的形式。可以计算 $ E_{21} A $ 检验是不是等于上图的第二个矩阵。

$$
\begin{equation}
\begin{bmatrix}
1&0&0\\
-3&1&0 \\
0&0&1 \\
\end{bmatrix}
\end{equation}
$$
同理，还有$E_{32}$，那么就能够构成整个消元的过程，容易看到，变换是满足结合律的
$$
U = (E_{32} (E_{21} A))
$$
可以组合起来得到
$$
U = E A
$$

这些$E_{xy}$是一个**初等矩阵(Elementary Matrix)**。什么是初等矩阵呢？它是一个和单位矩阵很接近的矩阵，表示由单位矩阵从一次初等变换得来的矩阵。

这里要区分初等矩阵和初等变换的概念，初等变换指的是：

交换某两行
某行乘以非零常数
把第 i 行加上第 j 行的 m 倍
这是一个三角矩阵，其中第 i 行 j 列的元素为 m。这里维基百科中文还写错了。

这里提前介绍了一点置换矩阵(permutation)。左乘表示行变换，右乘表示列变换。因此我们常常看到有$x^T A x$这样的变换方式，这种实际上是二次型，对行和列都会进行变换。
$$
\begin{equation}
\begin{bmatrix}
0&1 \\
1&0 \\
\end{bmatrix}
\begin{bmatrix}
a&b \\
c&d \\
\end{bmatrix}
=
\begin{bmatrix}
c&d \\
a&b \\
\end{bmatrix}
\end{equation}
$$

$$
\begin{equation}
\begin{bmatrix}
a&b \\
c&d \\
\end{bmatrix}
\begin{bmatrix}
0&1 \\
1&0 \\
\end{bmatrix}
=
\begin{bmatrix}
b&c \\
d&a \\
\end{bmatrix}
\end{equation}
$$

L03 矩阵乘法和逆矩阵

本章首先提出了矩阵乘法的五种看待方法，考虑矩阵乘法$A B = C$，其大小分别为$(m \times n) \times (n \times p) = (m \times p)$。
$$
A =
\begin{equation}
\begin{bmatrix}
1&3 \\
2&7 \\
\end{bmatrix}
\end{equation}
$$

第一种方法是最传统的，左边的行乘上右边的列，得到的是一个点。

第二种方法看做左边的矩阵，分别去乘上右边矩阵的每一列，这样得到$p$个列向量，然后把它们拼起来就能得到$C$。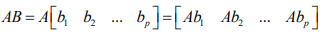

而每一列的值如下所示。也就是 AB 的第 p 列只和 B 的第 p 列有关，和 B 的其他列无关。B 的第 p 列的每个行元素，表示 A 的对应列的权重。然后这些列按照这个权重加起来。
容易看出，如果 B 的第 p 列中只有第 i 列为1，其他都为0，就相当于选择了 A 的第 i 列作为 AB 的第 i 列。

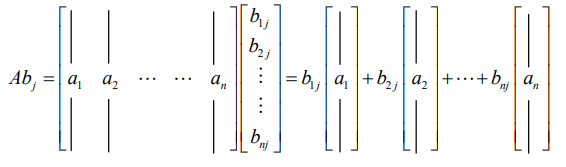
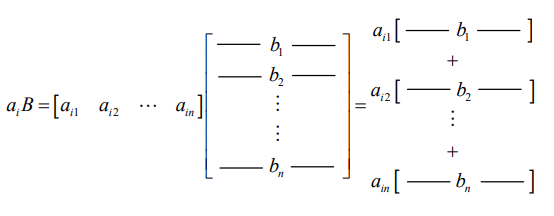
第三种方法看做左边的矩阵的每一行，分别去乘上右边矩阵，这样得到$m$个行向量，然后把它们拼起来就能得到$C$。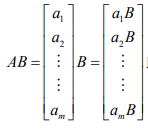

第四种方法看做左边的矩阵的每一列，分别去乘上右边矩阵对应的行，得到$n$个矩阵，然后将它们对应位置加起来就能得到$C$。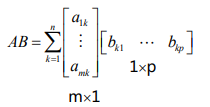

这一种方法，对于左边是由1和0组成的矩阵有特别的效果，就好像我在 pick 列一样。
$$
\begin{equation}
\begin{bmatrix}
a&b \\
c&d \\
\end{bmatrix}
\begin{bmatrix}
1 \\
0 \\
\end{bmatrix}
=
\begin{bmatrix}
a \\
c \\
\end{bmatrix}
\end{equation}
$$

第五种方法是分块矩阵。

对于方阵而言，左逆等于右逆$A^{-1} A = I = A A^{-1}$。
对于非方阵，则不然。毕竟连形状都不同了。

可逆矩阵又称为非奇异(non singular)矩阵。这里的奇异其实在一些场景中被翻译为“单”。

假设 A 乘上一个 B 可以得到单位矩阵 I，但实际找不到这样的 B。
$$
A =
\begin{equation}
\begin{bmatrix}
1&3 \\
2&6 \\
\end{bmatrix}
\end{equation}
$$

可以用矩阵的第二种乘法形式来理解，单看 $ [x , y]^T $那一列。

$$
\begin{equation}
\begin{bmatrix}
1&3 \\
2&6 \\
\end{bmatrix}
\begin{bmatrix}
x&* \\
y&* \\
\end{bmatrix}
\end{equation}
=
\begin{bmatrix}
1&0 \\
0&1 \\
\end{bmatrix}
$$

可以从线性空间角度理解，组成 A 的两个列向量构成一条直线，但 $ [1 , 0]^T $ 单位矩阵的第一列就不在这条直线上。

还可以从方程的角度理解。如果 A 不可逆，那么 $Ax = 0$ 存在非零解 $x$。

另外，在之前介绍消元的时候讲到过，如果出现全零行，那么矩阵不可逆。

高斯若尔当消元法求逆矩阵。

L04 LU分解

逆矩阵的特性，这个只要注意到$AA^{-1}=I$就可以了，教授用了一个经典的比喻，就是穿衣服先穿里面的，再穿外面的；那么脱衣服也要先脱里面的，再脱外面的。
$$
(AB)^{-1} = B^{-1}A^{-1}
$$
证明如下，然后用结合律就行了
$$
(AB) B^{-1} A^{-1}
$$
这其实反映了把矩阵作为变换的一种角度的思考。

转置的操作，相当于沿着主对角线翻转。

类似于逆，还有
$$
(AB)^T = B^T A^T
$$

这个证明不如矩阵的逆直观，因为转置没有 $AA^{-1}=I$ 这样的定义。不过可以通过下图来看。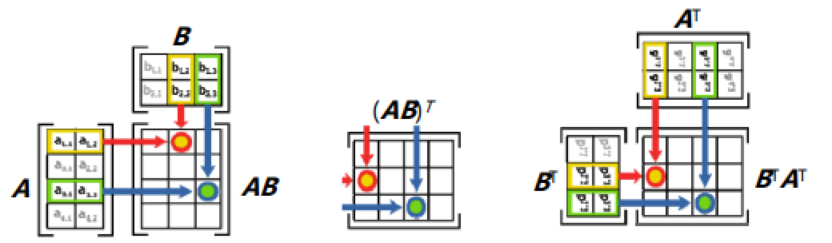

另外一个性质是
$$
(A^T)^{-1} = (A^{-1})^{T}
$$
证明是
$$
(AA^{-1})^{T} = (A^{-1})^T A^T = I
$$
关于逆和转置的性质，可以进一步从范畴论上来描述，但我目前还没怎么看懂。

LU 分解将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积。其中 L 的主对角线是 1，U 的主对角线未必是1。

$$
A = L U
$$

有时需要让主元出现在对角线上，所以要交换原矩阵的一些行，所以要再乘上一个置换矩阵P，称为PLU分解。

因为
$$
E_{32} E_{31} E_{21} A = U
$$
所以

$$
A = E_{21}^{-1} E_{31}^{-1} E_{32}^{-1} U
$$

LU 分解的意义是什么呢？我觉得应该是好算。从下图中教授的示例中可以看到，在计算 $ E_{21}^{-1} E_{32}^{-1} $ 时，下面一行的逆矩阵相乘互不干扰，所以基本上不需要计算就能得出来。而上一行的原矩阵则会干扰，比如会出现 10 这样奇怪的数字。这也是为什么要求逆的原因，这样可以快速得到 L。

用教授的话来说，只要把消元乘数填进来就得到 L，和 A 没有关系。这相比我们用消元的方法得到 L，显得非常优美。

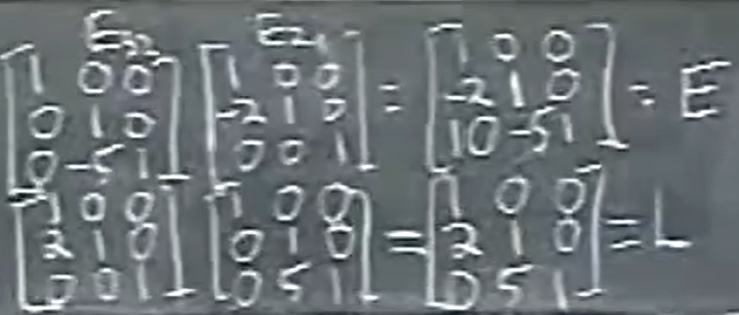
后面教授还进一步计算了下消元的复杂度，是 $O(n^3/3) 的$。

L05 转置与向量空间

置换矩阵$P$是对行重排的$I$，共有$n!$种。实际上它们对应置换群。
置换矩阵具有性质$P^{-1} = P^T$

这个性质可以从下面的图中获得直觉。可以发现 P 的第 i 行和 $ P^{-1} $的第 i 列相乘会得到1，和其他列相乘都是0。

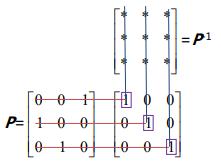
以 $i = 1$ 为例，$ P^{-1} $ 的第一列必然是

$$
\begin{equation}
\begin{bmatrix}
0 \\
0 \\
1 \\
\end{bmatrix}
\end{equation}
$$

而它也恰恰是 P 的第 i 行的转置。

对称矩阵定义是$A^T = A$，容易得到$R^T R$是对称的，证明就是用 $(AB)^T = B^T A^T$。

vector space 表示向量空间，它需要对加法和数乘封闭。
subspace 表示子空间。0向量一定在子空间里面，因为任何一个向量和0数乘都是0向量，而向量空间要对数乘封闭。或者从群论的角度，子群一定包含单位元。

两个子空间的交集一定是子空间，可以想象三维空间里面的一条线是一个子空间，那么两条线的交点一定也在这个三维空间里面。这个实际上是子群的性质。
比如下面我们证明对加法封闭：
$$
x \in U \wedge x \in V \\
y \in U \wedge y \in V \\
x + y \in U \\
x + y \in V \\
x + y \in (U \cap V) \\
$$

两个子空间的并集不一定是子空间，可以想象用两个向量做加法可以张成一个平面，但平面上的向量并不都在两个向量上面。

column space 表示列空间。列空间是由矩阵$A$的所有列向量生成的$R^m$上的子空间，记作 $C(A)$ 。例如下面的矩阵 $A$，实际上它 $ R^3 $ 中两个向量张成的平面。

$$
\begin{equation}
\begin{bmatrix}
1&3 \\
2&3 \\
4&1 \\
\end{bmatrix}
\end{equation}
$$

L06 列空间和零空间

可以从第 12 分钟开始看。

矩阵 $A$ 的列空间 $C(A)$ 中的所有向量，都为 $R^m$ 上的向量，即 $m$ 维向量。
列空间中的所有向量均为矩阵 $A$ 中列向量的线性组合。在后面线性相关性的讨论中，我们会将列向量组合成矩阵。

注意，后面的课程往往会和线性方程结合起来，列空间实际上是方程 $Ax = b$ 里面的解 $x$。但要注意，列空间的定义实际上是列向量的线性组合。

下面，将列空间和线性方程结合起来看。列空间用来描述 $Ax = b$ 这个方程的解 $x$。

考虑矩阵

$$
A =
\begin{equation}
\begin{bmatrix}
1&1&2 \\
2&1&3 \\
3&1&4 \\
4&1&5 \\
\end{bmatrix}
\end{equation}
$$

那么，什么情况下方程 $Ax = b$ 有解呢？当 $b$ 在 $A$ 的列空间中时，这个方程有解。原因很显然，列空间包含所有 $ Ax $ 能得到的向量。

所以其实列空间有两个描述，它既是列向量组成的空间，又是某个方程的解。

下面引入了线性相关的概念。对于上面的矩阵 A 中的三个列向量，有没有“滥竽充数”的呢？或者说如果是否可以去掉一个列向量，但是可以得到相同的列空间呢？答案显然，列3是列1和列2相加。我们称列3和列1列2线性相关。因此实际上 A 的列空间是 $R^4$ 上的一个二维空间。

null space 表示零空间。主要用来描述 $Ax = 0$ 这个方程的解。

同样举上面的例子，因为 x 是三维向量，所以零空间是 $R^3$ 的子空间。
我们能口算得到 $ [1 \,1 \, -1]^T $ 是一个解：

用左边矩阵的每一列，乘以右边矩阵的每一行
看成 x 的每个分量，分别数乘 A 的每一列

同样 $[n \, n \, -n]^T$ 都是解。这实际上是一条直线。
可以看到零空间中也存在线性相关的问题。

下面，教授证明了 $Ax$ 是向量空间，也就是证明如果 $ A(v) = 0, A(w) = 0$，则 $A(v+w) = 0, aA(v) = 0$。因为矩阵乘法对矩阵加法可分配。

【Q】因为0向量是单位元，看起来它很像是群论里面的 Ker 即核的概念。

现在我们回到列空间 $ Ax = b $，尝试求出它的所有解。比如我们令 b 为 $ [1 , 2 , 3 , 4]^T$
不妨先思考下，这些所有解是否构成向量空间了呢？那就不一定了。要看解里面是否包含0。

L07 计算 Ax = 0

在下面的例子中将 $Ax$ 转化为了 $Ux$。因为 $A$ 不是方阵，所以需要用消元法而不能使用 LU 分解。得到的是类似下面的阶梯(echelon)矩阵的形式。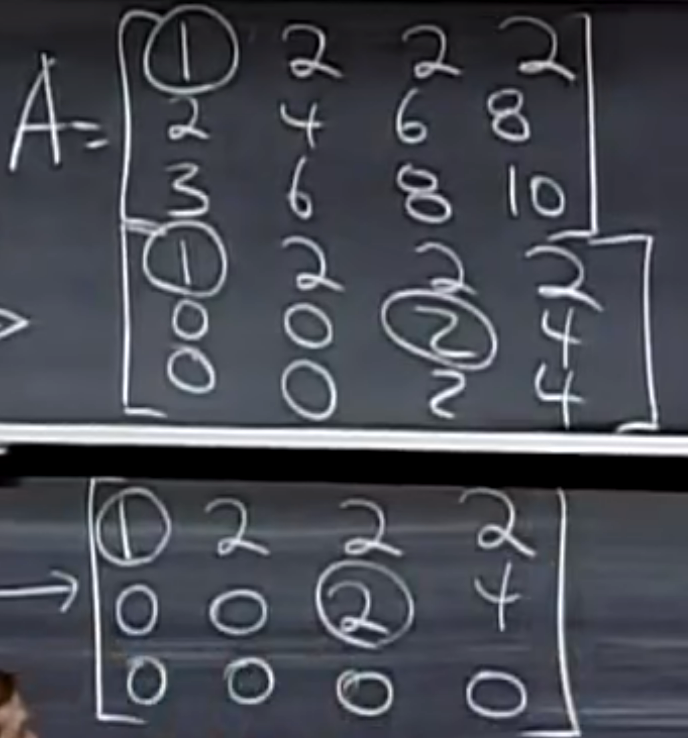

A 的主元(pivot)数量为 2，称为矩阵的秩(rank)。在这里可能产生困惑，因为之前只操作过方阵的主元。其实主元的定义是做行消元时某一行的第一个非零元。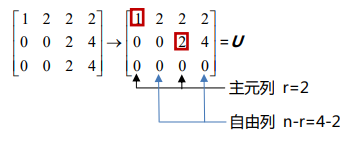

包含主元的列是主元列，否则是自由列。那么实际上可以给自由列上赋任意的值，然后求解主元列。例如，一般给其中一个自由列赋1，其他的赋0，能够得到如下两个特解。

$$
x_1 =
\begin{equation}
\begin{bmatrix}
-2 \\
1 \\
0 \\
0 \\
\end{bmatrix}
\quad
x_2 =
\begin{bmatrix}
-2 \\
0 \\
-2 \\
1 \\
\end{bmatrix}
\end{equation}
$$

【Q】能不能两个都赋值0？那一定得到0向量，0向量在任何子空间中，所以没啥意义。

通过特解可以构造出整个零空间。
$$
x = c x_1 + d x_2
$$

到这里可以理解秩的一个意义，令列 $ n = 4 $，秩 $ r = 2 $，说明只有两个方程起作用。

简化行阶梯形式(Reduced row echelon form)。也就是

让每个主元上方和下方都是0。
让主元变为1。

matlab 中通过 rref 指令可以得到简化行阶梯形式。

从下图中可以看到，简化行阶梯形式中可以找到单位矩阵 I 这样的构造。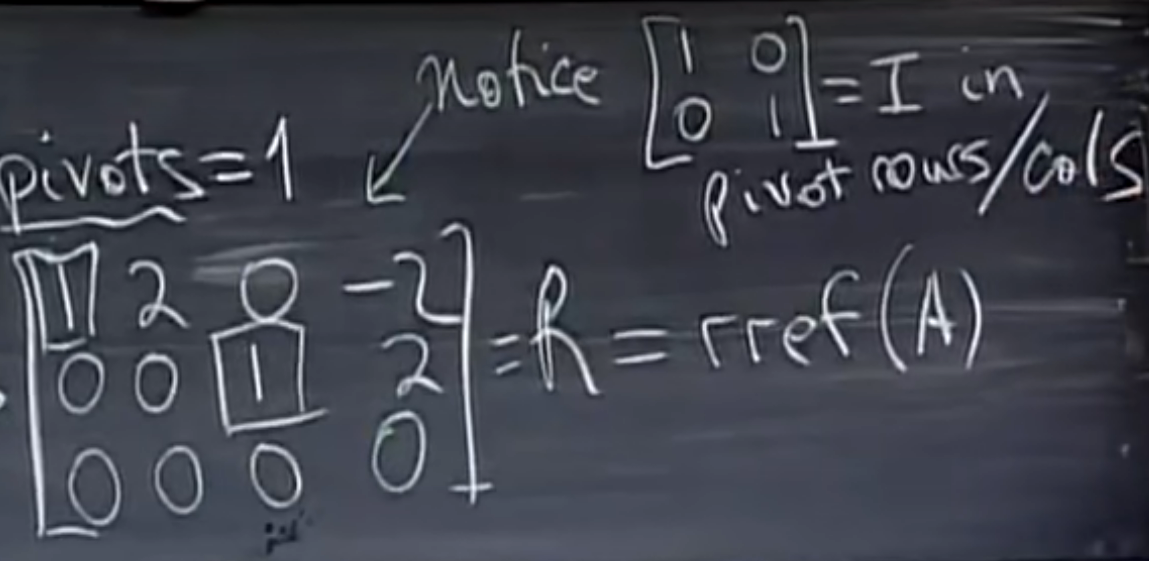

甚至可以将矩阵分为主元部分和自由部分。主元部分实际上就是 I。而自由部分未必是个方阵。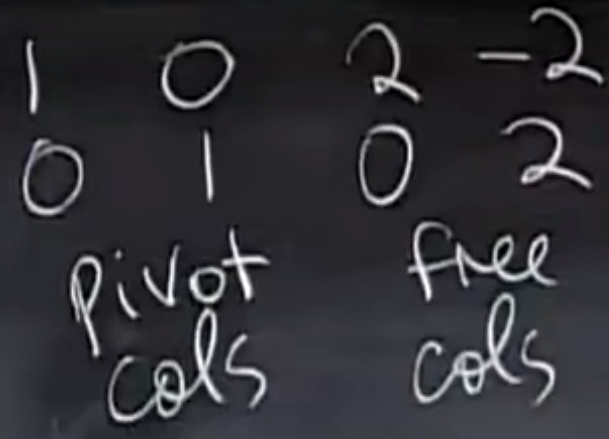

或者写成

$$
\begin{bmatrix}
I&F \\
0&0 \\
\end{bmatrix}
$$

观察上图，可以发现它和特解 $x_1$ 和 $x_2$ 有着对应的关系。主元部分 $I$ 相等，但自由部分 $F$ 相当于是取了两个特解的相反数。于是可以从特解直接构造出简化行阶梯形式(只要特解是按照一个自由列赋1，其他所有赋0来做的，不然得不到 $I$ 啊)。不过为什么是相反数呢？它是怎么来的呢？

现在先考虑构建一个零空间矩阵 $N$，它的各列由特解组成，显然我们希望
$$
RN = 0
$$

观察发现下面的 $N$ 满足条件，其中 $I$ 对应矩阵 $R$ 自由变量部分，$-F$ 对应矩阵 $R$ 主元部分。

$$
N =
\begin{equation}
\begin{bmatrix}
-F \\
I \\
\end{bmatrix}
\end{equation}
$$

如下图所示，$U$ 是一个“上三角”矩阵，它得到的 $R$ 是图中第二个矩阵。
那么 $RN$ 应该是0，我们不妨乘起来看看，也就是红色和红色乘，绿色和绿色乘。

L08 计算 Ax = b

增广矩阵(augmented matrix)。

$$
\begin{equation}
\begin{bmatrix}
1&2&2&2&b_1 \\
2&4&6&8&b_2 \\
3&6&8&10&b_3 \\
\end{bmatrix}
\iff
\begin{bmatrix}
1&2&2&2&b_1 \\
0&0&2&4&b_2-2b_1 \\
0&0&0&0&b_3-b_2-b_1 \\
\end{bmatrix}
\end{equation}
$$

有解的条件是 $ b_3-b_2-b_1 = 0 $。

首先讨论可解性。从向量空间的角度，$ Ax = b $可解的条件是当 $b$ 在 $C(A)$ 中。
所以，如果 $A$ 中的一些行是0，那么对应的 $b$ 也应该是 0。

然后找特解。相比零空间，这里只需要将所有自由变量设为0，解出主变量。其实在 $ Ax = 0 $ 中也可以执行这一步，只是解得0，最后通解的表示上也是加上 $b$，所以没意义。

$$
x_p =
\begin{equation}
\begin{bmatrix}
-2 \\
0 \\
3/2 \\
0 \\
\end{bmatrix}
\end{equation}
$$

然后求通解。这里是通解加上任意对应的零空间 $ Ax = 0 $ 中的解。这很符合直觉，因为如下所示，特解 $x_p$ 加上0，结果还是0
$$
A x_p = b \\
A x_n = 0 \\
A (x_p + x_n) = b
$$

即
$$
x_c =
\begin{equation}
\begin{bmatrix}
-2 \\
0 \\
3/2 \\
0 \\
\end{bmatrix}
+ c
\begin{bmatrix}
-2 \\
1 \\
0 \\
0 \\
\end{bmatrix}
+ d
\begin{bmatrix}
2 \\
0 \\
-2 \\
0 \\
\end{bmatrix}
\end{equation}
$$

不过为什么这包含了所有的解呢？下面教授展示了四维空间画二维平面的绝技。

设矩阵有 $m$ 行 $n$ 列。

容易看出，矩阵的秩一定小于等于 $m$ 且小于等于 $n$。
先前教授举的例子中，$r$ 都小于 $m$ 且小于 $n$，我们已经发现此时 $ Ax = b $ 无解或者有无穷多的解。
现在考虑列满秩情况，即 $r=n$。此时没有自由变量。$Ax = b$ 的解是0个或者1个。
现在考虑行满秩情况，即 $r=m$。此时消元不会有零行，并且存在一些自由向量。$Ax = b$ 始终有解。
现在考虑满秩的情况，即 $r=n=m$。此时方程有唯一解。

满秩矩阵 $r=n=m$ 经过消元变换，能够得到 $I$。满秩矩阵的列空间为0向量。【Q】总感觉这里能对应一些同态的概念，甚至是单群的概念？

【Q】其实感觉从这里开始的课程中就始终没有分清楚列秩和行秩。其实有个结论列秩等于行秩，虽然一直没有被提及或者证明。但因为后面都是讲的列向量组，所以一般都是列秩。

L09 线性相关

线性相关(dependence)，线性无关(independence)都是对向量组而言的。

什么情况下，向量 $x_1, x_2, …, x_n $ 线性无关呢？在系数不都为零的情况下，如果存在有线性组合为零向量，那么是线性相关的。
即存在下面的情况
$$
c_1 x_1 + c_2 x_2 + … + c_n x_n = 0
$$

零向量和任意向量 v 是相关的，因为能找到
$$
c_1 0 + c_2 v = 0
$$

给定平面上的三个向量，它们一定是线性相关的。如何一眼看出这个结果呢？我们可以将这三个向量 $v_1, v_2, v_3$ 组成一个2行3列的矩阵 $A$。可以发现这个矩阵存在一些自由变量，所以 $ Ax = b, b = 0 $始终有解 $x$。换句话说，在零空间里面，存在非零向量 $x$。
因此可以这样考虑，对于一些向量组成的矩阵 A，如果它的零空间 $Ax = 0$ 中只包含零向量，那么这些向量线性无关。
相反，如果零空间$Ax = 0$中包含除零向量之外的解，那么这些向量线性相关。

从 L03 矩阵乘法和逆矩阵中可以看到，如果 $Ax = 0$ 有非零解，那么A 矩阵不可逆。因此如果列向量们构成可逆矩阵，则线性无关，从而零空间只包含零向量。
这个定义是前几节课中不停考虑列向量的不同组合下，什么时候能等于0，什么时候会等于b。

还可以从秩的角度来看线性相关性。如果线性无关，那么所有的列都是主列。实际上所有的自由列都可以看做是主列的某种组合。

列向量张成(span)向量空间，表示这个空间由所有这些向量的组合构成。
容易想到，是否存在不多不少个列向量，它们既张成空间，但线性无关呢？这些向量称为基(basis)。
这里教授犯了一个错误，他说张成一个三维空间。其实可以发现有两行相同，所以消元一定能得到一个全是0的行，所以这三个向量其实还是线性相关的。实际上它们张成一个平面，没错，$ [3 , 3 , 7]^T $ 和 $ [3 , 3 , 8]^T $ 都在这个平面上。
$$
\begin{equation}
\begin{bmatrix}
1&2&3 \\
1&2&3 \\
2&5&8 \\
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
1&2&3 \\
0&4&5 \\
0&0&0 \\
\end{bmatrix}
\end{equation}
$$

这里教授说，只要方阵可逆，那么就是基。但他没有具体解释，所以这是为什么呢？

如果方阵可逆，那么它可以经过一系列初等变换，变为单位矩阵 I
这是因为在 L02 矩阵消元那一章讲过如果矩阵最下面一行都是0，没有主元，那么矩阵是不可逆的。那么可逆的矩阵一定可以经过消元得到一个 U，进而最后得到一个 I。
如果方阵可逆，那么表明 $Ax = b$ 有唯一解，从而秩为 $n$。

例：找出下列向量组的一组基

$$
\begin{bmatrix}
1&2&3&1 \\
1&1&2&1 \\
1&2&3&1 \\
\end{bmatrix}
$$

显而易见的是第一列和第二列构成一组基。这样后面两列是自由列。

$$
\begin{bmatrix}
1&2 \\
1&1 \\
1&2 \\
\end{bmatrix}
$$

下面给出定义，列秩是矩阵 $A$ 中主元列的个数，也就是列空间的维度。这里强调的是矩阵 $A$ 的列空间 $C(A)$ 而不是矩阵的维度。所以实际上它联系了矩阵和列空间。

对于上面的矩阵，考虑零空间的基。矩阵 $A$ 的零空间 $ N(A) $ 的维度是自由变量的数量。所以有对于 $m$ 行 $n$ 列矩阵来说，如果秩是 r，则 $n - r$ 是零空间的维度，即自由变量的数量。

L10 四个基本子空间

这节课从教授纠正了上节课的那个错误开始。他说课后的学生说，因为她发现 $A$ 不可逆，所以列向量线性相关。

教授随后说，其实还能发现两个行相等，所以其实只能当做一个行。因此在这里行的性质也反映了列的性质。这也就引入了本节课四个子空间之一的行空间。

设 A 是 m 行 n 列的矩阵。A 的四个子空间分别是：

列空间 $C(A)$
列向量的线性组合。方程 $Ax = b$ 的解 $x$ 的集合。
这些空间为什么被叫作子空间呢？之前提到过，列空间指的是 $m$ 个列向量生成的 $R^m$ 上的子空间。
零空间 $N(A)$
方程 $Ax = 0$ 的解 $x$ 的集合。
因为包含了 $ Ax = 0 $ 的所有解，而 $x$ 是 $ R^n $ 上的，所以零空间是 $R^n$ 的子空间。
行空间 $C(A^T)$
行向量的线性组合。也可以看做 $A^T$ 的列空间。是 $R^n$ 的子空间。
左零空间 $N(A^T)$
是 $R^m$ 的子空间。

项目	$C(A)$	$N(A)$	$C(A^T)$	$N(A^T)$
矩阵的秩/空间的维数	$r$	$n-r$	$r$	$m-r$
基	主列	$Ax = 0$ 的特解，或者自由向量	前 $r$ 行阶梯型行向量	$E$ 中和 $R$ 中0行对应的行(看后面讲解)

下面是对这个表格进行讨论的几个话题。

首先是零空间 $N(A)$ 的基为什么是 $Ax = 0$ 的特解？
教授帮我们回忆，每个特解都是从一组自由列得出的。

这里教授直接讲了行秩等于列秩，所以 $C(A^T)$ 也是 $r$。但他也说了这里缺一个证明，估计是没讲。

$C(A)$ 不等于 $C(R)$，也就是说进行行变换消元之后得到的列空间不同。比如下面的例子中，$[1 , 1 , 1]^T$ 属于 $C(A)$，可显然它不属于 $C(R)$。

$$
\begin{equation}
\begin{bmatrix}
1&2&3&1 \\
1&1&2&1 \\
1&2&3&1 \\
\end{bmatrix}
\rightarrow
\begin{bmatrix}
1&0&1&1 \\
0&1&1&0 \\
1&0&0&0 \\
\end{bmatrix}
\end{equation}
$$

这里我感到有点困惑，看了下 randomwalk 的笔记，他也有类似的困惑。他的解释是，初等矩阵的行变换并不会改变线性相关性。证明也很简单，假设 $A$ 秩为 $r$，则前 $r$ 个列向量线性无关。消元操作实际是 $EA = U$，即 $E [a_1, … a_r] = U$。后面假设线性相关则有 $ c_1 E a_1 + c_2 E a_2 + … + c_r E a_r = 0$。

那么经过行变换得到的列，还在行空间中么？答案是显然的。因为消元是一系列行变换，而行变换可以看做线性组合，显然经过线性组合之后，向量还在同一个行空间里面。

下面教授介绍了如何计算 $N(A^T)$ 的基。他给出了一种非常巧妙的方式。
首先，先介绍左零空间为什么叫左零空间？所以相当于是 $y$ 左乘了 $A$。

$$
A^T y = 0 \Leftrightarrow y^T A = 0
$$

然后切入正题，考虑扩展一下之前的高斯若尔当消元法

$$
rref ([A_{m \times n} \quad I_{m \times m} ]) \Rightarrow [R_{m \times n} \quad E_{m \times m} ]
$$

因为消元法本身只是行变换，所以这个运算是能够进行到最后得到某个 $E$ 的。实际上经过对应的行变换，$E$ 如下所示

$$
\begin{bmatrix}
-1&2&0 \\
1&-1&0 \\
-1&0&1 \\
\end{bmatrix}
$$

现在来考虑 $E$ 的意义。

$$
EA = R
\\
\begin{equation}
\begin{bmatrix}
-1&2&0 \\
1&-1&0 \\
-1&0&1 \\
\end{bmatrix}
\begin{bmatrix}
1&2&3&1 \\
1&1&2&1 \\
1&2&3&1 \\
\end{bmatrix}
=
\begin{bmatrix}
1&0&1&1 \\
0&1&1&0 \\
0&0&0&0 \\
\end{bmatrix}
\end{equation}
$$

教授说，我们看 $R$ 矩阵只有最后一行为0，所以 $E$ 矩阵的最后一行就是 $N(A^T)$ 的基，它确实是1维向量。为什么呢？不妨把这最后一行单独拿出来，根据矩阵乘法的第三个性质，我们可以得到如下的式子

$$
[-1 , 0 , 1] A = [0 , 0 , 0 , 0]
$$

即

$$
x^T A = 0
$$

两边转置一下，就是

$$
A^T x = 0
$$

而这个的解 $x$ 就是零空间。而因为之前教授讲过，零向量的一组特解就是零空间的基。

对于上面表格的讨论到此为止，下面是一些新的内容。
这里教授讲到，其实矩阵本身就可以构成一个向量空间。
比如 3x3 的矩阵，它的子空间是上三角矩阵或者对称矩阵。这两个子空间的交集是对角矩阵。可以直觉写出对角矩阵的基。

$$
\begin{equation}
\begin{bmatrix}
1&0&0 \\
0&0&0 \\
0&0&0 \\
\end{bmatrix}
\begin{bmatrix}
1&0&0 \\
0&3&0 \\
0&0&0 \\
\end{bmatrix}
\begin{bmatrix}
0&0&0 \\
0&0&0 \\
0&0&7 \\
\end{bmatrix}
\end{equation}
$$

L11 矩阵空间和小世界图

对角矩阵构成的子空间 $S$ 维数为6。上三角矩阵构成的子空间 $U$ 维数为6。
介绍矩阵的和，或者叫直和。
考虑矩阵 $S$ 和 $U$，它们的交集是一个空间，但是它们的并集不一定是一个空间，这个之前已经讲过了。定义直和是 $s_i + u_j$，其中 $i$ 和 $j$ 取遍 $S$ 和 $U$ 中所有可能的元素。它是 $M$ 的子空间。我们实际上有如下类似容斥原理的等式
$$
dim(S) + dim(U = dim(S + U) + dim(S \cap U)
$$

下面的矩阵秩为1。根据矩阵乘法的第四种表示形式，它可以被分解为一个列矩阵乘以一个行矩阵。
$$
\begin{bmatrix}
1&4&5 \\
2&8&10 \\
\end{bmatrix}
$$

一个 5x17 的秩为 4 的矩阵可以被分解为 4 个秩为 1 的矩阵。

设 M 为所有 5x4 的矩阵，求所有由秩为 4 的矩阵构成的子集是子空间么？显然不是，因为0矩阵不在里面。那么如果加进去呢？也不是。因为我们有
$$
dim(S) + dim(U = dim(S + U) + dim(S \cap U)
$$
因此两个秩为4的矩阵加起来的秩未必是4了。

在 $R^4$ 空间中，所有满足 $v_1 + v_2 + v_3 + v_4 = 0$ 的向量构成子空间 S 么？是构成的，因为它肯定是某个矩阵的零空间。这个矩阵秩肯定是1，因为只有一个方程，对应是一个一行的矩阵。

实际上我们可以把矩阵写出来 $ [1, 1, 1, 1]$。

这个矩阵的左零空间维数是 $m - r = 0$，所以特解应该只包含零向量。
对这个一列的矩阵消元，易于发现它的列空间是1，而秩是1，同样可以算出左零空间维数是0。
$$
\begin{equation}
A^T =
\begin{bmatrix}
1 \\
1 \\
1 \\
1 \\
\end{bmatrix}
\end{equation}
$$

L12 网络

这里教授插了一句，零空间的含义就是如何线性组合列向量 $x$，从而得到0。其实也同时解释了 $ Ax = 0 $ 这方程的含义。

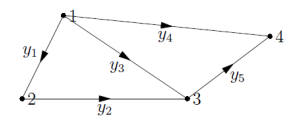
上面的一张电路图，我们可以转成一个关联矩阵(incidence matrices)。其中4列对应4个节点，5行对应5条边。

$$
\begin{bmatrix}
-1&1&0&0 \\
0&-1&1&0 \\
-1&0&1&0 \\
-1&0&0&1 \\
0&0&-1&1 \\
\end{bmatrix}_{5 \times 4}
$$
从矩阵上来说，矩阵的前三行线性相关。教授说这表明 $y_1$、$y_2$、$y_3$三条边在图上构成一个环，看一眼图，确实不错。有环如何导致线性相关呢？这里我觉得可以想象成向量的加法。

现在考虑 $A$ 的零空间。首先 $Ax$ 是什么？是电势差。

那么 A 的基是什么呢？$ [1, 1, 1, 1]^T$ 是一个基，大家电势都相等，Ax 肯定是0。教授说实际上接下来 $dim(N(A)) = 1$，所以基就是那一个。

所以零空间实际上是一维，也就是一条直线。这在物理意义上表示每个点的电势由一个常数决定，但如果我们比如将点4接地，也就是令它的电势为0，那么就可以求出其他的电势。

这里感觉教授直接跳过了列空间，毕竟 $ Ax = b$ 的意义很明显，就是给定电压求电势。

这一段主要讲基尔霍夫定律。

$$
\begin{equation}
A^T=
\begin{bmatrix}
-1&0&-1&-1&0 \\
1&-1&0&0&0 \\
0&1&1&0&-1 \\
0&0&0&1&1 \\
\end{bmatrix}_{4 \times 5}
\end{equation}
$$

不妨看看 $A^T y = 0$ 的物理意义。我们可以列出第一个方程 $-y_1-y_3-y_4=0$，表示点 1 的合电流是 0，也就是流入等于流出。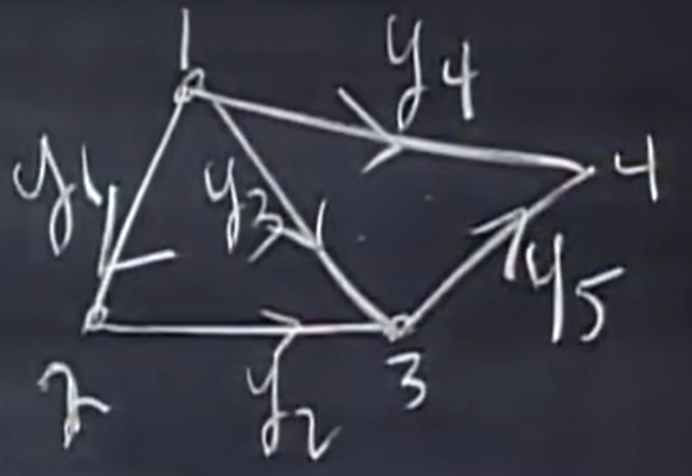

下面求这个零空间的基。因为矩阵的秩是 3，所以要找两个特解。GS 老板肯定又不想消元，而是口算了。他这次的做法是分别令右边和左边回路的电流为0，然后就得到两个特解。当然，我们令 $y_3$ 为0，就可以求出大回路对应的特解。

$$
\begin{equation}
y_1=
\begin{bmatrix}
1 \\
1 \\
-1 \\
0 \\
0 \\
\end{bmatrix}
y_2=
\begin{bmatrix}
0 \\
0 \\
1 \\
-1 \\
1 \\
\end{bmatrix}
\end{equation}
$$

为什么我们选择回路来求特解呢？结合前面的讲解，构成回路的向量是线性相关的。从上面的基 $y_1$ 也能看出，它实际上说明了前三行如何组合得到0。

下面看下 A 的行空间。

首先，哪些列可以是基呢？用先前回路的方法，可以看出 1/2/3 和 3/4/5 分别线性相关。所以教授选了 1/2/4 作为主列。从图中看到，1/2/4 构成的子图没有回路，这也意味着它们线性无关。

进一步，可以得到
$$
|loop| = |edge| - (|nodes| - 1)
$$

其中括号里面的是秩，它等于 $n-1$。为什么秩一定是 $n-1$ 呢？这是之前讲的电路的性质，也就是零空间只有一维。

其实这个性质对所有的图都成立。它就是欧拉公式，太神奇了。注意多面体的欧拉公式和我们图论中的欧拉公式还不一样。

之前讲的是无外部电源的基尔霍夫定律。如果加入外部电源，无非就是变成 $ A^T x = f$，其中 $f$ 是输入的电流。

教授借此介绍应用数学中最基本的方程

$$
A^T C A x = f
$$

留下一个问题下面的矩阵有什么特性？他们都是对称的。

$$
A^T C A
$$

L13 复习

这一章是复习，我没看视频，对着题目做了。

Q1

这一题比较 trivial，就不说了。

Q2

这一题比较 trivial，就不说了。

Q3

如何用行最简阶梯矩阵的性质求出矩阵 A 呢？其实我当时是先看答案得到 A，然后求出 R 再恍然大悟的。这里 tricky 的一点是要列交换。

这里秩为1，自由向量为2。两个通解写成 N 的形式是

$$
\begin{bmatrix}
1&0 \\
1&0 \\
0&1 \\
\end{bmatrix}
$$

这一点不像 $ [-F, I]^T$ 啊。所以我们交换两列，将 I 放到第一个主元的位置就行

$$
\begin{bmatrix}
0&1 \\
0&1 \\
1&0 \\
\end{bmatrix}
$$

然后就可以得到

$$
\begin{bmatrix}
1&0&-1 \\
0&0&0 \\
0&0&0 \\
\end{bmatrix}
$$

看起来不对啊，因为之前我们交换了两个自由列，所以在构造 R 中要再换回去。如下所示，就对了

$$
\begin{equation}
R =
\begin{bmatrix}
1&-1&0 \\
0&0&0 \\
0&0&0 \\
\end{bmatrix}
\end{equation}
$$

判断题时间：

如果方阵 A 的零空间中只有零向量，那么它的转置的零空间是什么？
肯定只有零向量，因为 $n=m$，所以 $N(A)=n-r=m-r=N(A^T)$。
所有 5x5 可逆方阵是否构成 5x5 矩阵空间的子空间？
取巧的办法就是检查零向量，果然不在里面。
如果 $B^2$ 为0，则 $B$ 是否为0？
不。
方程组 $Ax=b$ 具有 $n$ 个方程 $n$ 个未知数，若矩阵 $A$ 的列向量线性无关，则 $b$ 取任意向量，方程均有解。
是，有唯一解。

Q4

$$
B = C D =
\\
\begin{equation}
\begin{bmatrix}
1&1&0 \\
0&1&0 \\
1&0&1 \\
\end{bmatrix}
\begin{bmatrix}
1&0&-1&2 \\
0&1&1&-1 \\
0&0&0&0 \\
\end{bmatrix}
\end{equation}
$$

第一小题求 B 零空间的一组基。这里题解说因为 C 可逆，所以 B 的零空间和 D 的零空间相同。这个就很有意思。randomwalk 说，左乘可逆矩阵等于对行向量进行可逆的线性组合。既不改变行空间，又不改变零空间。

第二小题求通解，首先因为向量 b 和矩阵 C 的第一列列向量完全相同，所以问题变为 $ Dx = [1, 0, 0]^T$。这里其实就是矩阵的第四种乘法。

笔记里面的做法是因为之前已经求出 B 的一组基了，所以可以直接用。但我的做法是直接从 b 推导。

$$
DN = b
\\
\begin{equation}
\begin{bmatrix}
1&0&-1&2 \\
0&1&1&-1 \\
0&0&0&0 \\
\end{bmatrix}
N =
\begin{bmatrix}
1 \\
0 \\
0 \\
\end{bmatrix}
\end{equation}
$$

因为 D 已经是行最简阶梯矩阵 R 了。而秩为2，行3列4，显然矩阵不满秩，它的 R 可以表示为

$$
D = R =
\begin{equation}
\begin{bmatrix}
I & F \\
0 & 0 \\
\end{bmatrix}
\end{equation}
$$

容易看出，前两列是 R 的前两列是行空间的基，后两列是自由变量即零空间的基。所以可以得到

$$
\begin{equation}
N =
\begin{bmatrix}
1&-2 \\
-1&1 \\
1&0 \\
0&1 \\
\end{bmatrix}
\end{equation}
$$

解释下，上两行是 -F，下两行是 I。然后再求出一个特解就行。

判断题：

A 为方阵，则它的行空间和列空间相同？
肯定不是，trivial。
如果 A 和 B 的四个子空间相同，则 A 一定是 B 的倍数？
错误，A 和 B 的可以为同阶可逆方阵。比如 6x6 的矩阵，那么它的行空间和列空间是整个 $R^6$，而两个零空间是0维。但它们不一定相同。
开放问题：如果 A 和 B 的是个子空间相同，则有什么性质呢？
对上一个问题进一步考虑，如果我们对矩阵 A 中的两行做行交换，四个子空间中不变的是哪些？
是行空间和零空间。这个在 L10 中我们接触过。
为什么向量 $v = [1,2,3]^T$ 不可能既在矩阵 A 的零空间中，又成为 A 的一个行向量

线性代数复习——以MIT18.06为指导