本文被拆分自分布式一致性和分布式共识协议。拆分的目的是:
- 上一篇文章更贴近于 DDIA 的架构
- 本篇文章理论性较强,可以单独被拆出
分布式系统上的一致性
在这个章节中,主要介绍和一致性相关的一些概念,包括:
- Consistency
- Order
- Clock
- Broadcast
从概念上:
- 分布式中的一致性指的是 CAP 中的 C
从外部看来,要求多副本的系统的行为表现得像单系统一样,并且对这个系统的修改是原子的。 - 事务一致性指的是 ACID 的 C
强调事务前后不变量不能改变。
本章节中会涉及到一些复制的内容,但详细有关复制的会在分布式一致性和分布式共识协议中论述,也是部分基于 DDIA 的。
最终一致系统
首先考虑为什么需要 Replicate 呢?可以列出下面的理由:
- Fault Tolerance
- Scalability
- Latency
没错,通过复制可以允许在不同地区设置 Replica,从而让用户就近选择。
然后必须意识到同步复制很难实现,因为这样单个节点的宕机,或者网络分区就会导致这个系统不可用。
但如果使用异步复制,那么要我因为一个异步的 Follower 节点可能落后,所以如果从这个节点读,就可能读到旧数据。例如,如果在 Leader 和 Follower 上跑相同的查询,就可能读到不同的结果,尽管这个过程是暂时的。这就是所谓的最终一致。
这里的最终是很模糊的,因为它并没有一个明确的 deadline。
下面,介绍最终一致系统中可能存在的一些问题,并引入一些“弱一致性”来解决对应的问题。
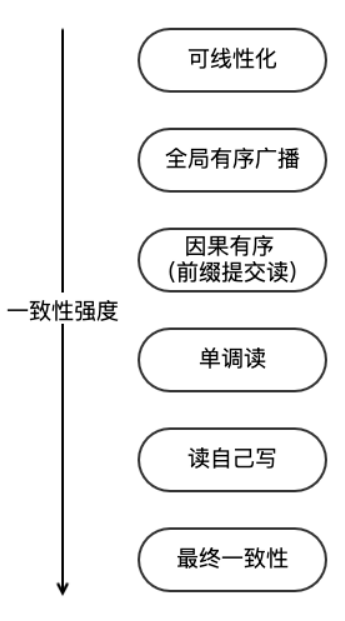
有的时候系统保证在更新操作后的一段时间后,系统能够达到一致性状态,这称为弱一致性。弱一致性和强一致性的区别是弱一致性存在“不一致窗口”,在不一致窗口中系统不一定保证用户总能看到最新的值。弱一致性可以分为最终一致性、因果一致性、单调读一致性、单调写一致性、有界旧一致性、前缀一致性等。
在Azure Cosmos中将一致性的强弱程度建立以下的关系。Strong–Bounded staleness–Session–Consistent prefix–Eventual。从前向后的延迟。可用性和扩展性越好,但一致性会差一点。
最终一致性
最终一致性也被称为乐观复制(optimistic replication),要求当没有新的对 X 的提交发生时,最终所有对 X 的访问都返回最后一次更新的值。
常见的异步复制的主从架构实现的是最终一致性。它的一个典型常见是用户读取异步从库时,可能读取到较旧的信息,因为该从库尚未完全与主库同步。注意,同步复制的主从架构会出现任一节点宕机导致的单点问题。
最终一致性通常用来提供 BASE 语义。
最终一致性是一种获得 HA 的常见方式。
读己所写一致性(Reading Your Own Writes)
读己所写一致性又称为 read-after-write consistency,
这里的己,指的是客户端。如下图所示,读己所写一致性要求客户端总能读到自己最新提交的写入。读己之写一致性不对其他用户的更新做出承诺。
如下图所示,用户写了一些 (1234, 55555, ‘Sounds good’) 到 Leader,Leader 返回了 insert ok 后,从 Follower1 和 Follower2 读。发现居然读不到自己刚写入的值了。这个场景下,读己所写一致性就遭到了破坏。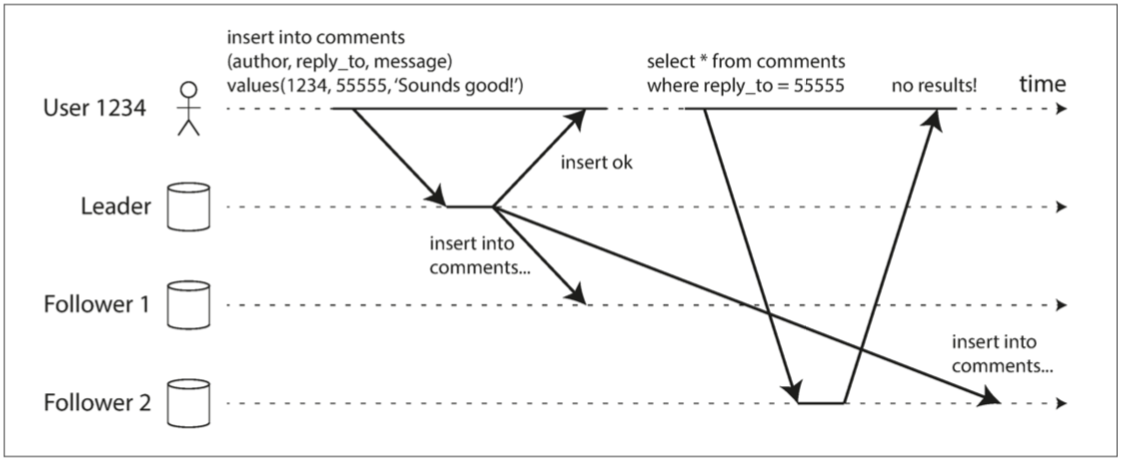
读己所写一致性可以通过以下的一些方式实现:
- 当读取可能被修改过的内容时,强制从主库读。
- 对于大部分内容都可能被修改的系统来说,上面的方案其实效率很差了。此时可以跟踪上次被更新的时间,并强制在上次更新后的某段时间内强制从主库读取。
- 客户端维护最近一次写入的时间戳,系统只从至少拥有该时间戳的修改的从库中进行查询。
我理解这类似于 Hologres 的一些做法,比如每次写操作返回一个 LSN,然后下次带着这个 LSN 再去读。 - 当数据副本分布在多个数据中心时,可能带来额外的复杂性。因为这些请求可能要跨越数据中心,直到被转发给 Leader。
单调读一致性(Monotonic Reads)
单调读一致性要求客户端在已经读到某个数据的某个版本之后,不可能在稍后的读中读到该数据先前的某个版本。
如下图所示,User2345 首先从 Follower1 读到了 55555 这个评论,但是在稍后的对 Follower2 的读中却没有读到。这是因为 Follower2 此时还没有收到 Leader 异步复制过来的日志。令 User2345 读 Follower1 的时刻为 X,则 User2345 在晚于 X 的一个时刻读取到了数据早于 X 时刻的版本,这违背了单调读一致性,即发生了时光倒流的“现象”。
这种时光倒流的原因是用户先查询了一个延迟很小的从库,然后又去查询一个延迟很大的从库。
实现单调读一致性的一种方案是确保每个用户从同一个副本进行读取,例如可以 Hash 用户的 ID 到不同的节点上。
DDIA 指出单调读一致性介于强一致性和最终一致性之间。在读数据的时候,可能读到旧的数据。单调读一致性保证了如果一个用户先后做了一些读,那么它不会再读到更新的数据后再读到更旧的数据。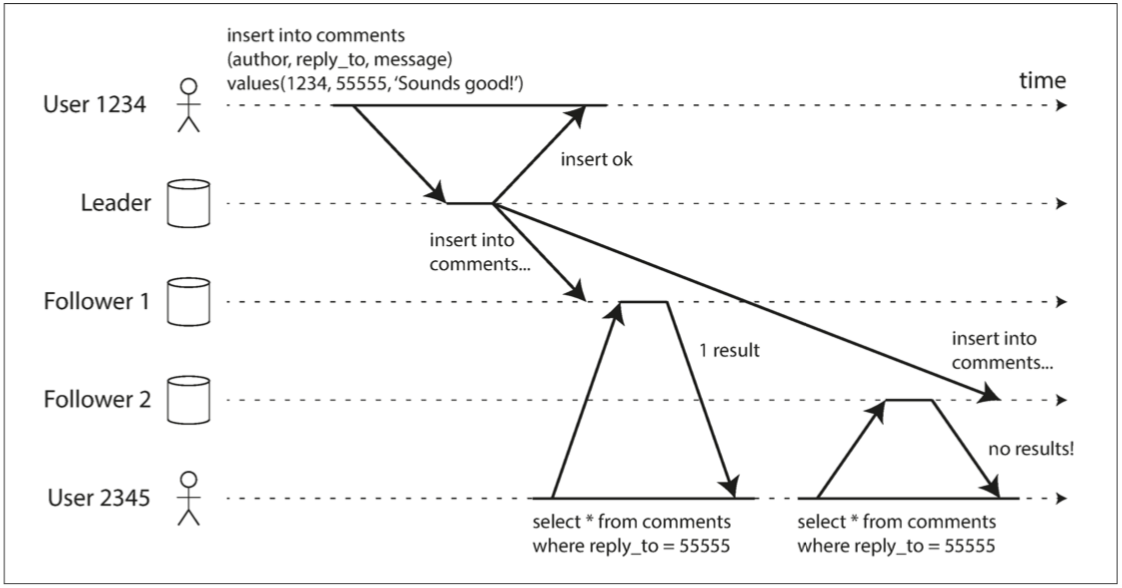
我个人的理解,单调读一致性相比于强一致性,免去了写入对读取的影响。
一致前缀读(Consistent Prefix Reads)
DDIA 中列出了一个例子,其中第三者看到回答先于问题。这是一个很奇怪的现象。
1 | Mrs. Cake |
如下图所示,因为 partition 1 比 partition 2 复制地慢,这就导致了一个 observer 看到了颠倒的顺序。
一致前缀读要求如果一系列写入按照某个顺序发生,那么任何人在读取时,也会读到同样的顺序。
一致前缀读的要求,体现在 partitioned/shared 数据库中。在这样的数据库中,不同分区是独立运行的,所以不存在全局写入顺序。为了解决这个问题,可以强制所有带有因果的写入都在相同的分区上。当然,也可以采用一些显式跟踪因果关系的算法,可以参考后面的 happen before 部分。
Multi Leader 复制和 Leaderless 复制在一致性上的相关问题
单 Leader 的问题是只有一个 Leader 能处理写,可用性差。
Leaderless 的问题是没有 Leader 来定序了。
在另一篇文章中讲解。
其他的一些一致性
可调一致性(RWN一致性)
诸如 Cassandra 的系统在最终一致性的基础上提供了可调一致性。对于任何读写操作,系统允许用户配置成功写操作的最小节点数 W、成功读操作的最小节点数 R 和副本节点的数量 N。可以根据读写请求的数量来动态调整可用性 C 和一致性 A 之间的 trade-off。
RWN 一致性存在不少问题,在另一篇文章中讲解。
会话一致性
会话一致性能够保证在该会话内一致前缀读、单调读、单调写、读己所写、write-follows-reads 一致性。
有界旧一致性
有界旧一致性(Bounded staleness)保证了读到的数据和最新版本最多差 K 个版本。
强一致性
根据 DDIA,线性一致性(Linearizability)常常也被称作强一致性(Strong consistency)、外部一致性(External consistency)、原子一致性(atomic consistency),所以这让线性一致性的定义很微妙。不妨看一下定义:
- CAP 理论的定义是 all nodes see the same data at the same time。
- Wait-Free Synchronization 的定义是 each operation appears to execute instantaneously, exactly once, at some point between its invocation and its response。
- DDIA 的定义是 the basic idea is to make a system appear as if there were only one copy of the data,
and all operations on it are atomic。
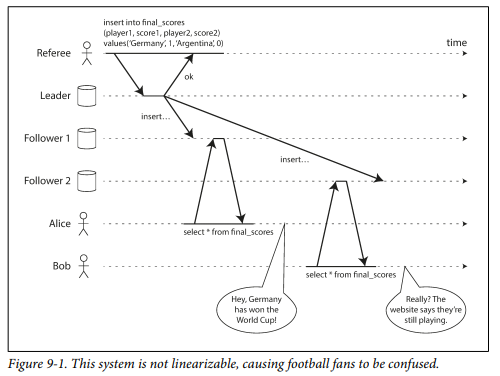
在下图中比赛结果由 Referee 写入 Leader 主库,并向两个 Follower 同步复制。当任何一个读取返回新值后,所有后续读取都必须返回新值。但简单的读写分离主从复制,就会出现当 Leader 只同步了 Follower1 而没有同步到 Follower2 时,对两个副本的读取结果分别返回新值和旧值的现象。
需要注意,线性一致性和“未提交事务不可见”不是一个概念。比如如下图所示,client B 读取到的 register x 的值可能为 0 或 1。因为此时 B 读和 C 写是并发的。按照线性一致的定义,只要在 invocation 和 response 之间瞬间完成读和写就行。
如果一个写入返回后,读取还能返回旧值么?当然是不行的,也就是下图中最后一个读一定要返回 1 了。因为 “… at some point between its invocation and its response”。所以在 response 后,这个操作就应该被认为已经执行完毕了。在 DDIA 中这样说到:
If the read started after the write ended, then the read must have been processed after the write, and therefore it must see the new value that was written.
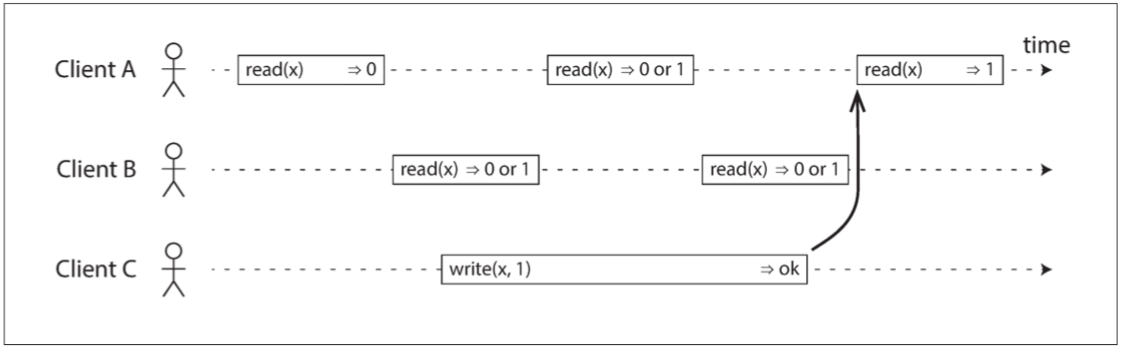
但是仅仅上面的例子还不足以说明 Linearizability。刚才知道了如果 read 和 write 是并发的,那么读是可以返回新值或者旧值。但是 Linearizability 也不允许读到的值在新值和旧值之间“左右横跳”。因为这现象通常是由于查询不同的节点导致的,所以这就体现出 single copy of the data 这个定义了。比如,如图所示,一旦 B 读到了 x 为 1 返回给客户端了,后续就不能读到之前的 x 为 1 的状态了。
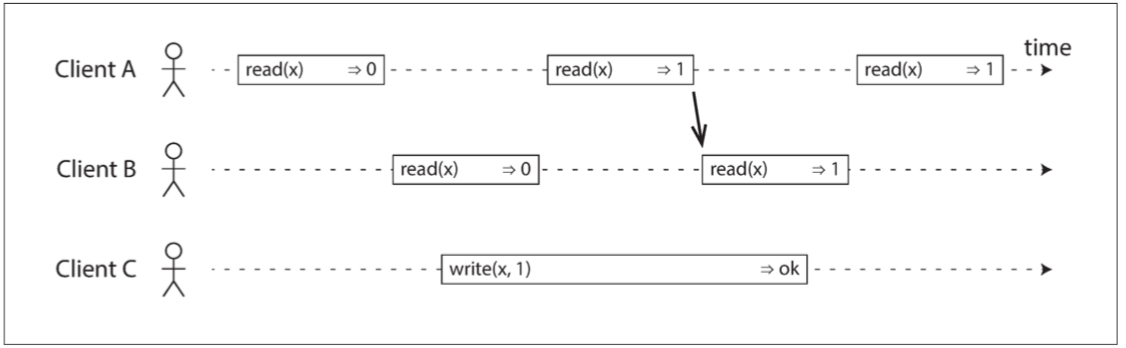
下图中的每个操作中都画了一条竖线,这表示这个操作实际被执行的时间。这些竖线是有序的,并且能够构造出对 register 的一个合法的读写,也就是每次读都是最近一次写入的值。Linearizability 的一个要求是连接这些竖线的斜线是始终向前的,也就是说读不能回退。
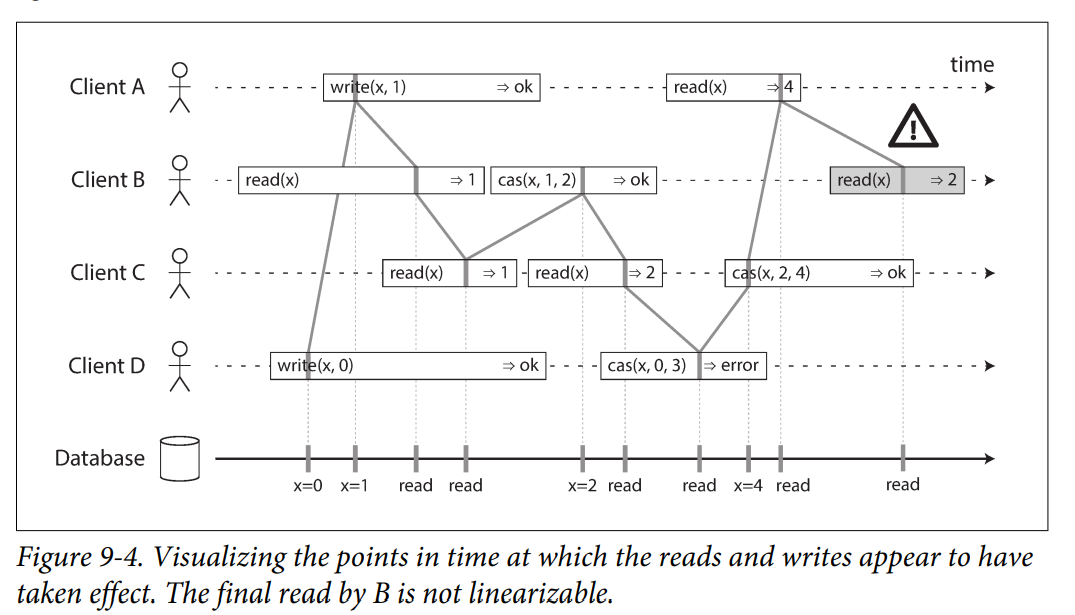
关于这个图有几点说明:
- Client B 先请求读 x,然后 Client D 写 x 为 0,然后 Client A 又设置 x 为 1,结果 B 返回的是 1,并且是 A 写入的 1。这是 OK 的,说明处理顺序是 D、A、B。尽管这不是用户发出请求的实际顺序,但这个执行顺序是 ok 的。
- Client B 先收到 x 为 1,Client A 稍后才收到自己写入 x 成功。这个也是合理的,这不代表是先读了 x,再写了 x,而是代表了给 Client A 的回复稍微晚到了点。
- 这个模型并不包含任何 transaction isolation。其他的 Client 可以随时修改变量的值。例如 Client C 先读到 x 等于 1,又读到 x 等于 2,这是因为在两次读取之间,值被 B 改变了。可以用 CAS 来避免这种情况。
- 感叹号下面的灰色方框中的读不是 linearizable 的。这是因为 Client A 已经返回了 CAS 的结果,即 4 了。
通过线性一致性可以实现分布式锁、选举、和唯一性约束等功能。我们使用共识算法实现的是线性一致性,而主从复制则不是。由此可见,分布式一致性(Consistency)和共识(Consensus)是完全不同的两个概念,后者是实现前者的一个工具。
Relying on Linearizability
强一致性对应了下面的一些场景
Lock 和 Leader 选举
选举 Leader 的一个场景是使用 lock。每个 node 都尝试获取 lock,但只有成功获得 lock 的 node 称为 leader。这个过程一定要是 linearizable 的,因为所有的 node 必须对谁持有锁取得共识。
对于诸如 Zookeeper 和 etcd 之类的协调服务,它们都需要依赖一个 linearizable 的存储。
Constraints and uniqueness guarantees
数据库中的唯一性约束依赖于可线性化。这同样类似于 lock 的场景,也类似于 CAS 的场景。
Cross-channel timing dependencies
辨析 Linearizability、Serializability
还需要区分Linearizability 和 Serializability。
Linearizability
Linearizability 来源于分布式系统和并发编程,其语境是 single-operation, single-object, real-time order,线性一致性保证了
- 写操作一旦完成,对后续的读操作是可见的,也就是经典的写后读问题。
- 一旦某个读操作返回了某个特定值,那么后续的读操作要么返回这个值,要么返回后面的写对应的值。
线性一致性往往对应于 CAP 中的 C,线性一致性是 composable,即 local 的。即如果每一个对象上的操作是线性的,那么系统上的所有操作都是线性的。
不同于 Serializability,Linearizability 并不会将操作们组合成一个事务,所以会产生诸如 Write Skew 的问题,除非使用一些物化冲突的办法,可以参考数据库系统中的事务。
Serializability
Serializability 来源于数据库,其语境是 multi-operation, multi-object, arbitrary total order,它是一个有关事务的保证,涉及一组操作。它保证了在多个对象上执行的多个事务等同于某个序列化的执行过程。听起来贼绕,可以对应着可串行化理解下。Serializability 相当于 ACID 中的 I,如果用户的每一个事务都能保证 correctness 即 ACID 中的 C,那么顺序执行的事务也能保证 correctness。
不同于 Linearizability,Serializability 本身不给事务的执行顺序加上任何的 real-time 约束,也就是不需要操作是按照真实时间严格排序的。Serializability 也不是 composable 的,它也不表示任何的确定性的顺序,它只是要求存在一些等价的执行序列。
Strict Serializability
Serializability + Linearizability = Strict Serializability 或者说 strong one-copy serializability(strong-1SR)。此时,这个事务可以被 serial 地执行,并且这个 serial order 是 real time 的。比如我发起一个事务 T1,它会写 x;然后发起另外一个事务 T2,它会读 x。Strict Serializability 要求 T1 一定在 T2 之前,并且 T2 要读 T1 的写。对照来看,如果只是 Serializability 的话,那么 T2 可以在 T1 前面。
DDIA 中提到,2PL 或者 actual serial execution 是 linearizable 的。
Serializable Snapshot Isolation (SSI)
注意,关于快照隔离的内容,可以参考事务隔离性介绍
Serializable snapshot isolation detects write skew by tracking the causal dependencies between transactions
SSI 并不是 linearizable 的:
However, serializable snapshot isolation is not linearizable: by design, it makes reads from a consistent snapshot, to avoid lock contention between readers and writers. The whole point of a consistent snapshot is that it does not include writes that are more recent than the snapshot, and thus reads from the snapshot are not linearizable.
总而言之,一个 consistent snapshot 中不会包含比这个 snapshot 更新的写入,那么从这个 snapshot 去读,就不是 linearizable 的,因为没有能读到最新写入的数据了。
线性一致与提交顺序
对复制自动机进行乱序提交有可能破坏线性一致,这是因为复制自动机按顺序执行日志本身就暗示了一种全序关系,只有从同样的初始状态,apply 同样的操作序列,才能保证得到同样的操作结果。乱序执行,相当于重新定序。给出如下的讨论:
各个副本之间的 apply 顺序不同。
例如日志中 key 的顺序是 A B C,结果 store 1 乱序提交是 A -> C -> B,store 2 是 B -> A -> C,那么此时一个客户端去读不同的 store,返回的结果是不一样的。
那么如果 client 带着一个 index,只有这个 index 被 apply 完才能读。这样能解决问题么?答案是不行。实际上无法获得一个快照,其中的每个 key 要么是最近一次写入,要么在它之前的写入都已经被 apply。
如下所示,所有的 key 都在被并行 apply,A1 表示 A 的第 1 个版本,圆括号中的表示还没有被 apply。假设 A1 和 C1 在同一时间被 apply 完毕。对于这个场景,如果在 A1 被 apply 完时取 snapshot 读,那么 C1 之前有 B1 没有被 apply。因为 C1 都能读到了,B1 却不能读到,不满足线性一致。1
A1 (B1) C1
同理,如果等 B1 apply 完了再取 Snapshot 读,那么此时取到的 Snapshot 可能像下面这样了。D1 就和刚才的 B1 一样了。
1
A1 B1 C1 (D1) E1
以上是 KV 的场景,如果引入事务层,能解决一部分问题。也就是通过事务层能够区分不相干的 key,然后让它们之间并行。例如写 A 和 写 B 不冲突。写 A1 和写 A2 冲突。写 A 和读 B 不冲突。写 B 和读 [A, C) 冲突。等等。
单纯在 Follower 上串行 apply,但是 Leader 上依然并行,可以解决问题么?
答案是不行。如果 Follower 不处理读,并且通过某一种方式能够确定一种偏序关系,让并行的写彼此不冲突,那么不会导致数据上的不一致。但如果 Follower 处理读,那么它可能返回和 Leader 不一致的序,因为合理的偏序关系不止一个。
诸如 MultiPaxos 或者 ParallelRaft 的一些实现允许这么做,主要原因是事务层在往共识层写的时候就保证了共识层的乱序不会产生问题。例如 TiKV 的事务层中有 Scheduler,它维护了一些 Latch,保证了在 Prewrite 这样的先读后写操作前,先对 key 对应的 Latch 上锁。这就保证了不同事务的 Prewrite 等写入是互斥的,同一时间只有一个能成功。这个锁只有在 Prewrite 执行完之后才会释放,而此时 applied_index 一定是已经 advance 过了。
Replication 模型和 Linearizability
- Single-leader replication
这可能是 Linearizability 的。
如果我们只从 Leader 或者同步复制的 Follower 读的话,那么还是有可能是 Linearizability 的。因为需要考虑分布式事务的情况。 - Consensus algorithms
这是 Linearizability 的。 - Multi-leader replication
这不是的。 - Leaderless replication
大概率不是的。
RWN 一致性可能在 w + r > n 的时候达到,但 DDIA 说这个也要看如何定义强一致。
参考“Leaderless Replication”,里面列出了6种可能破坏线性一致性的情况。可以发现,这些场景主要和实现的具体方式有关。但无论如何,要通过 RWN 来实现线性一致是比较困难的。我认为存在两个主要困难:- 在 Leaderless 的架构下,没有 Leader 去定序产生的。
对此,我认为可以仿照一些数据库事务的实现方式,在 write 前去请求一个全局的 TSO 服务,获得全局唯一递增的时间戳。这样可以避免在 DDIA 中花大篇幅讨论的 time-of-day clock 问题。 - 本身还是异步复制,所以访问不同的节点,可能读到陈旧的值
如“Linearizability and quorums”中所述。
- 在 Leaderless 的架构下,没有 Leader 去定序产生的。
Spanner 的 External Consistency
外部一致性由 Spanner 引入。
在实现外部一致性时,需要考虑写后读一致性(read-after-write consistency)和单调读一致性。也就是不能写完还读不到,或者读到旧的。由于分布式系统是多副本的,所以实现起来需要进行设计。
考虑一个例子:事务1在节点1写入数据 A,事务1完成后,事务 B 在另一个节点2写入数据 B。在这个场景下,A 和 B 并不是并发的。在上面这个过程中,有一个并发事务读取 A 和 B,那么它读取A和B的相对顺序是什么呢?例如如果他读到了B而没有读到A,可以认为外部一致性被破坏了。
为了解决外部一致性要求的顺序问题,一个简单粗暴的办法是所有事务的序列号都通过一个统一的中心节点分配。例如 Spanner 就使用了原子钟进行授时。为了解决原子钟的误差问题,我们可以在事务提交时,等待误差这么久的余量。
CockroachDB 通过逻辑时钟解决物理时钟太过接近,导致难以排序的问题。逻辑时钟的概念,可以参考 Lamport 时钟。
顺序、因果和时钟
因果一致性(Causal consistency)
因果一致性要求如果 A 在因果上先于 B,那么 A 一定先于 B 被提交。在实际场景中可以表现为 B 依赖 A 的结果、A happens before B 等。
因此,因果一致性实际上是偏序的,如果 A 和 B 之间没有先后关系,那么 A 和 B 就是可以以任意顺序被提交的。可以看出,因果一致性是比线性一致性要弱的一个一致性,因为线性一致要求全序关系,而因果一致性是偏序的。线性一致性隐含了因果一致性,任何线性一致的系统都能保证因果一致。在单核单线程上的因果一致就是线性一致,这是因为整个程序是顺序执行的。
从 Ordering 的角度理解线性一致,那么线性一致系统中是不存在并发操作的。所有的操作都能在同一条时间线上构成一个全序关系。
ZAB 协议中使用因果一致性。
Ordering and Causality
顺序有助于保持因果关系:
- 在一致前缀读中,问题是因,回答是果。问题和回答之间存在 casual dependency。
- 在 Figure 5-9 中
这个场景中,update 依赖 insert,但却先于 insert 到达。这违背 Causality,因为一行要先被 insert,然后才能被 update。 - 在 Detecting Concurrent Writes 中
A 和 B 之间可能有的关系是 A happen before B,或者 B happen before A,或者 A 和 B 是 concurrent 的。这里的 happen before 也是一种 Causality,因为如果 A happen before B,则 B 可能依赖 A,或者知道 A 的信息,或者是基于 A 构造出来的等等。反之,如果是 Concurrent 的,那么两者之间没有因果关系,A 和 B 彼此互相不知道。 - 在 Snapshot Isolation 中
作者说,a transaction reads from a consistent snapshot。这里的 consistent 的意思是 consistent with causality。如果这个 snapshot 中包含 answer,那么一定包含 question。所有 happen before 这个 snapshot 的操作都可见,所有 happen after 的都不可见。
而 Read skew 即 Non Repeatable Read 场景下,就违背了因果。 - 在 Write skew 场景下
- 在线性一致的定义中,TODO。
The causal order is not a total order
- Linearizability
在 linearizable 系统中,操作之间存在全序关系,如果系统表现得只有一份副本,并且所有的操作都是原子的,那么任意两个操作都可以排个先后。如 Figure 9-4。 - Causality
因为存在 concurrent 关系,所以 causal order 只是 partial order。一些操作之间不能互相比较。
Linearizability is stronger than causal consistency
Linearizability implies causality。
让一个系统 linearizable 可能损害性能和可用性,特别是系统中存在客观的网络延迟的情况下,比如它是跨地理空间分布的。所幸 Linearizability 并不是唯一可以保证因果的方法。实际上因果一致性可能是最强的不会被网络延迟影响的模型,在网络失效的情况下,也能 available。
捕获因果关系
Concurrent 操作可以以任何顺序被执行,但是如果操作 A happen before B 的话,在所有 replica 上都要按照这个顺序来执行。
In order to determine the causal ordering, the database needs to know which version of the data was read by the application. This is why, in Figure 5-13, the version number from the prior operation is passed back to the database on a write. A similar idea appears in the conflict detection of SSI, as discussed in “Serializable Snapshot Isolation (SSI)” on page 261: when a transaction wants to commit, the database checks whether the version of the data that it read is still up to date. To this end, the database keeps track of which data has been read by which transaction.
Sequence Number Ordering
如何在分布式系统中捕获因果关系,或者说确定因果顺序呢?相比维护一个有向图,使用序列号或者时间戳的方案会更加容易。由于在集群中维护以现实为标准的物理时钟的性价比是较低的,而节点之间只需要在需要共同访问的时间的先后顺序上达成一致。时间戳未必是日历时钟,也就是所谓的 time-of-day clock 或者 physical clock。而更有可能是一个逻辑时钟,例如一个单调递增的计数器。当然,这样的计数器给实际上 concurrent 的事件也赋予了全序关系,这可能有些过强了。
如果使用 single leader replication,那么这个 replication log 为 write 操作定义了一个全序关系,这个全序关系和 causality 是一致的。Leader 可以简单为每个 operation 自增 counter,然后为 replication log 中的每个 operation 分配一个单点自增的 sequence number。Follower 只要按序 apply 掉 replication log 中的写入,就可以保证状态是因果一致的,哪怕它落后于 leader。
当然,在分布式环境下,维护一个全局的单调计数器可能比较困难。比如我们并不是使用 single leader replication,或者此时网络中有了分区。此时有一些优化方案:
- 每个节点自增,但加上节点的的 tag
比如某个节点只使用奇数编号,另一个节点只使用偶数编号。 - 使用物理时钟,再加上一些 LWW 的 confliction resolution 策略
- 为每个计数器分配对应的区块
但按了葫芦起了瓢,上面这些方案并不能实现因果一致:
- 如果有的计数器很快,有的很慢,那么生成的值是无法比较的
比如一个奇数编号更大,未必说明它比偶数编号更新 - 物理时钟可能有 clock drift
下面会介绍 Lamport clock,以及后来加强版 Vector clock 这两个逻辑时钟,通过它们可以实现因果一致。
Lamport Clock
Lamport Clock 或者 Lamport timestamp,定义如下
- 在同一进程中,如果 a 先于 b 发生,那么 C(a) < C(b)
注意**反过来是不成立的**。一个平凡情况,就是进程 p1 上面有一个事件 a,LC(a) 是 1。另一个进程 p2 上面发生了非常多的事件 b1..b100,b100 的 LC(b100) 是 100。两个进程没有任何交互。那么肯定是没有 happen before 的关系。
下图中列出了另一个 case
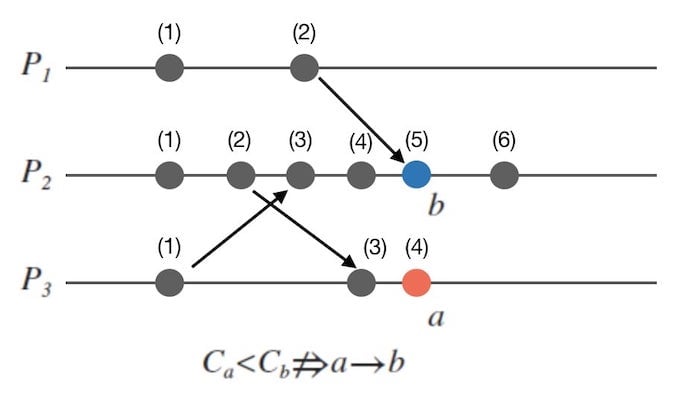
注意,虽然反过来不成立,但是也不会有C(a) < C(b)且b -> a的现象了。 - 如果消息 M 从进程 P1 发送到进程 P2,令 P1 的发送事件为 a,P2 的接收事件为 b,有C(a) < C(b)
- 如果 C(a) < C(b),C(b) < C(c),则 C(a) < C(c)
这也是传递性
Lamport Clock 实际上描述了happen before关系。
Lamport时钟的算法可以被描述如下。注意Wikipedia与诸如文章1和文章2在表述上有一些冲突,但看下面的图发现说的是一个意思。说法的不同是:
Wikipedia是把事件产生和事件发送拆开来说的,产生一个事件+1,发送不加,收到+1。例如原始状态是0,产生一个事件是1,发出去还是1,收到之后要+1,变成了2。
另外两篇文章说的是我一个事件产生完就立马发送了,这整个过程中,+了1。
事件在当前节点发生
1
time = time + 1;
发送事件
1
send(message, time);
接收事件
1
2(message, time_stamp) = receive();
time = max(time_stamp, time) + 1;
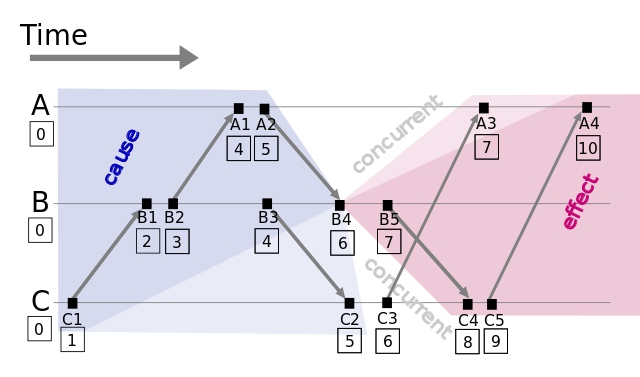
Lamport Clock 得到了偏序关系,但是我们可以从这个偏序关系整理出若干种全序关系(一个常用的方式是按照进程号进行排序),虽然真实发生的是其中的一种情况。在下图中展示了 B4 这个事件的“光锥”。蓝色部分的是因,红色部分的是果。
总而言之,可以按照下面的办法生成全序关系:定义 a -> b 为,其中 -> 表示 Happen before 而不是蕴含关系(implication):
1 | Ci (a) < Cj (b) |
其中 C 表示逻辑时钟,P 表示进程号,i/j 表示进程,a/b 表示进程上的事件。
下面看看为什么 a -> b,则 C(a) < C(b):
- 如果 a 和 b 位于同一个进程内,显然是成立的
- 如果 a 和 b 位于不同进程 i 和 j 中,那么必然在事件 a 到事件 b 之间有一次从i到j的通信
不妨把这次通信c->d画出来,其中 c 可能为 a,d 可能为 b。
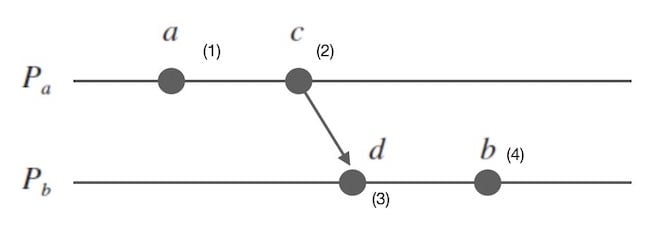
容易发现 a/c,c/d,d/b 之间都会伴随着 Lamport Clock 的自增。
通过逻辑时钟,可以解决对共享状态访问的竞态问题了,因为可以对所有 a -> b 这样存在 happen before 关系的时间赋一个逻辑时间戳了。但诸如节点故障单点问题等问题还需要容错机制来解决。
Lamport 时钟的缺点
首先,如果 A -> B 即 A happen before B,则 C(A) < C(B),但是对 Lamport 时钟来讲,反之并不成立。
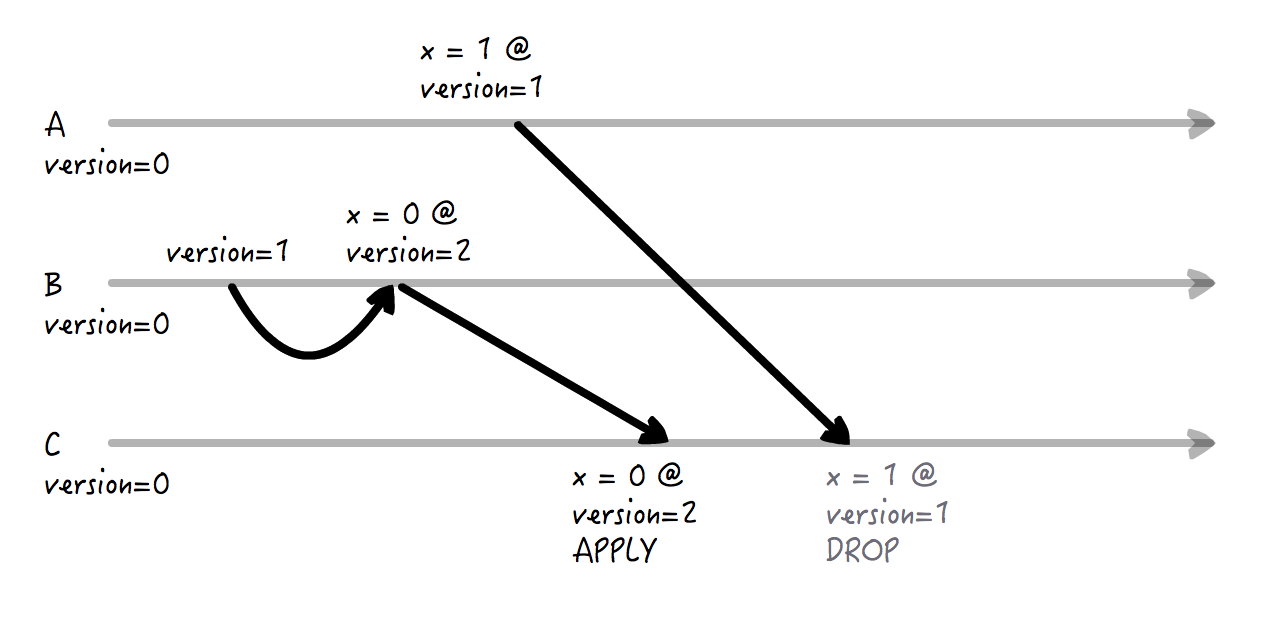
其次,它并不能识别 a 和 b 不存在 happen before 关系的情况。如下图所示,A 和 B 上面的事件是平行发生的。当他们都发送消息给 C 后,因为 B 的逻辑时钟更大,所以 A 的消息被丢掉了。
但这个合理吗?站在上帝视角看到,其实 A 事件的“物理时间”上是比 B 要更晚的。如果走物理时钟,应该把 B 的消息丢掉!当然,这种平行时空的问题,本来就是婆说婆有理,公说公有理的,所以这是一个时钟冲突。这样的冲突不好解决,但 Lamport Clock 并不能识别出这种冲突,这是问题所在。我们希望的是 Lamport Clock 能够在这种情况下能够判断出冲突,而不是武断认为 B 更靠后发生。
因此,我们有了Vector Clock,它能够识别出平行事件。
Lamport 时钟扩展:计算机中的时钟
NTP
在计算机系统中,NTP 协议被普遍用来进行授时。
授时的核心在于计算两个终端之间的 clock drift。计算方式在libutp源码简析这文章中已经介绍过了。这个方案有个很强的假设,就是认为网络是对称的,即 A->B 和 B->A 的时间是对等的。
Lamport Clock
如何在分布式系统中实现更靠谱的授时呢?其实在分布式系统中,只是需要知道事件发生的全序关系而不是具体的时刻,自然想到了Lamport时钟。
在 Lamport 时钟中,我们根据发送和接收消息可以确定某些事件之间的偏序关系。剩余的互相处于“平行时空”的事件咋办呢?可以根据所处进程号进行排序。这个在之前讲过了,就不再赘述。
Vector Clock(VC)
向量时钟针对 Lamport Clock 做了两点改进:
- 提出了 vector clocks ordering,能够识别平行关系
- 允许
VC(A) < VC(B)则A -> B的反向推理
vector clocks ordering
首先介绍一下 vector clocks ordering:
T=T'
等于关系表示两个向量的每个对应元素都相等。T<=T'
……都小于等于。T<T'
T<=T'且非T=T',也就是说只要有一个不等于,那就是小于。T||T'
平行关系,既不T<=T',也不T'<=T。
向量时钟的一个作用是发现数据冲突,也就是所谓的 version clock。
规则
假设分布式系统中有 N 个进程,每个进程都有一个本地的向量时间戳 T[i]。它是一个向量,其中 Ti[j] 表示进程 i 知道的进程 j 的本地的向量时钟值。特别地,对于进程 i 来说,Ti[i] 是进程 i 本地的向量时钟值。
向量时钟算法实现如下:
- 当进程 i 当有新的事件发生时,自增向量时间戳
Ti[i]。 - i 发送消息前需要自增
Ti[i]。也就是认为发送是一个事件。
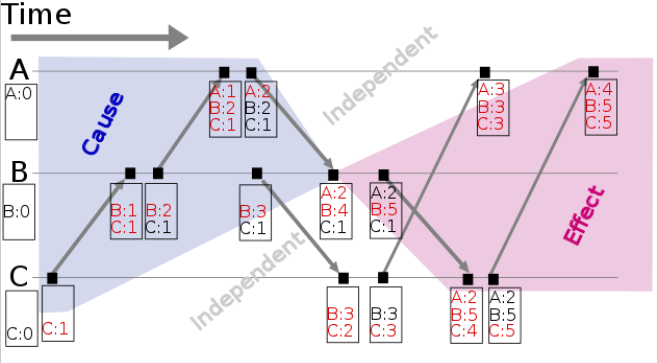
可以从下图看到,B 在接收完 C: 1 后产生的是 B: 1 C: 1。 - 当进程 i 发送消息时附带自己的向量时间戳 MT=Ti,这是一个向量。
- j 接收消息后需要立即自增
Tj[j]。也就是认为接收是一个事件。 - 在上一步后,接受消息的进程 j 更新本地的向量时间戳 Tj
更新方法很简单,zip 一下自己的 Tj,以及来自 i 的 MT 这两个向量,哪个大取哪个。1
2for k = 1 to N:
Tj[k] = max(Tj[k], MT[k])
应用:判断因果关系
如何使用向量时钟判断两个事件的因果关系呢?不妨先看两个进程比较的情况。在这里把事件的下标放到进程前面,这是为了方便后面推广。
进程 i 和 j 上发生了事件 a 和 b,它们的向量时钟分别为 Ta 和 Tb。Ta[i] 表示进程 i 知道事件 a 时的时间戳。
- 如果
Ta[j] < Tb[j]- 如果
Ta[i] > Tb[i]则 a 和 b 同时发生,记作a <-> b
也就是进程 j 上面 a 的时间戳小于 b,但是进程 i 上面 a 大于 b。看上去是个矛盾,这也表明两个事件时同时发生的。 - 如果
Ta[i] <= Tb[i]则 a happens before b,记作a -> b
- 如果
推广和证明
上面只是涉及了两个进程,可以推广下,证明对于事件 A 和 B,如果 VC(A) < VC(B) 则 A -> B。
令 VC(A) = [m, n],VC(B) = [s, t],由 VC(A) < VC(B) 可以得出:
- m <= s。
- n <= t。
- 两个等号不会同时成立,这是因为收发消息也算事件。
不妨画一张图,Pa 表示事件 A 所在的进程,Pb 表示事件 B 所在的进程。如果说 m < s,那么肯定在不早于 A 和不晚于 B 时,A 往 B 发了消息,也就对应了下图的 [m1, n1] 和 [s1, t1]。不然的话,这个更大的 s 是哪里来的?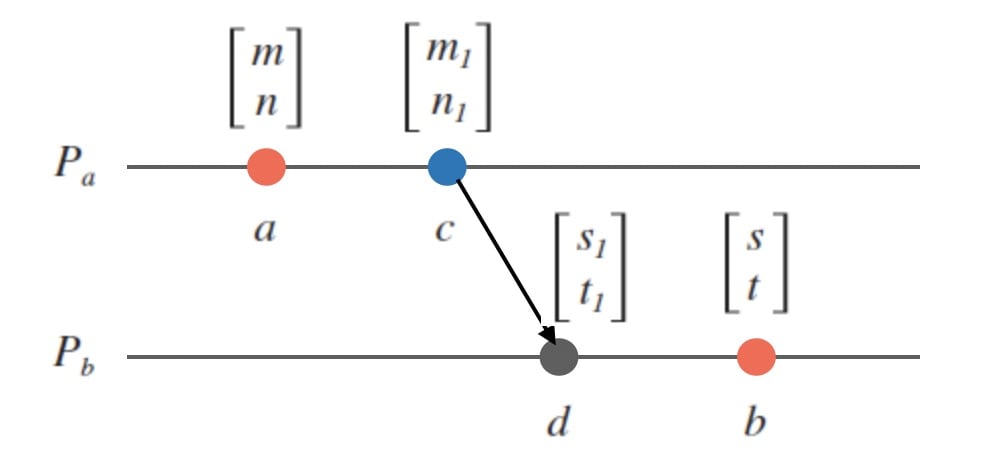
大于等于 m 的 s 可能来自如下图所示的4种不同的情况,实际上图只是一个。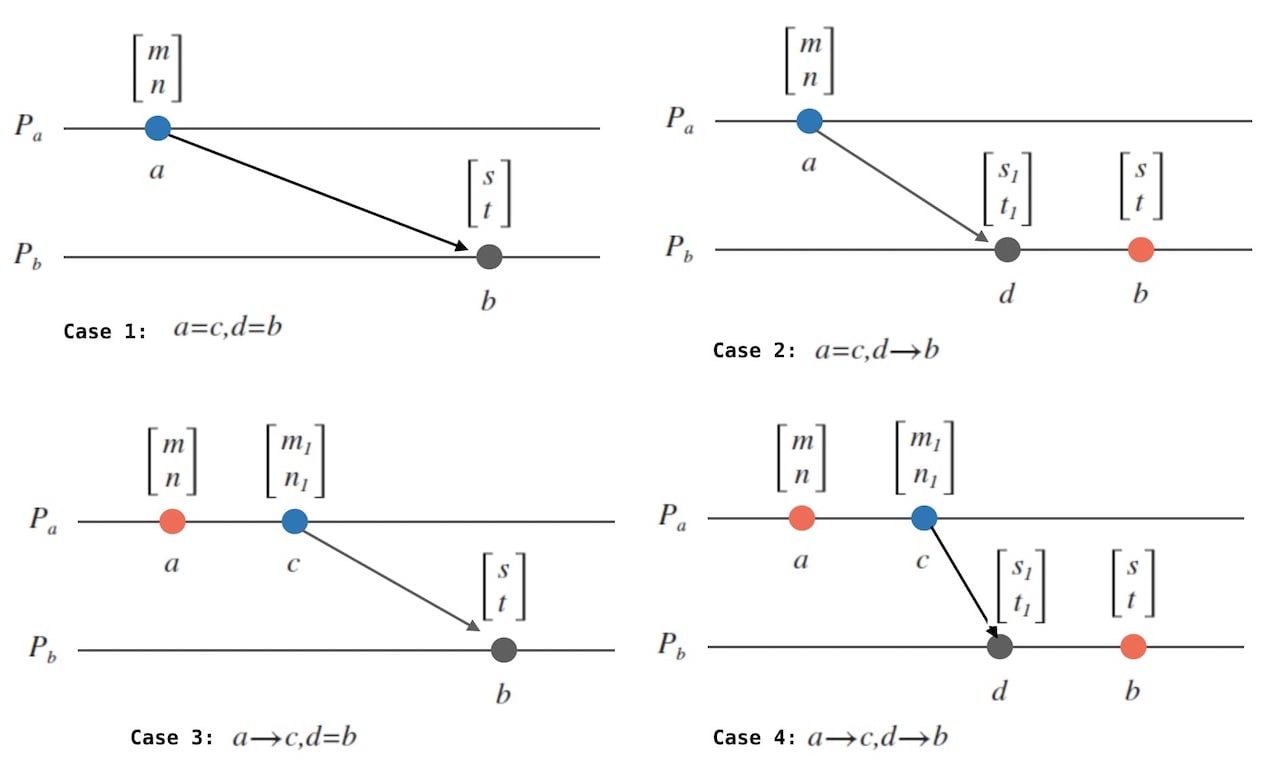
能不能只用 Vector Clock 呢?
我觉得是可以的,但这样就是完全依靠通信来同步。通信是不可靠的,如果通信链路上拥塞,或者干脆隔离了,那么系统就不可用了。
此外,对一个 N 节点的集群,每个节点需要维护长度为 N 的向量,并且每次发送消息也得是这个长度。
TrueTime
TrueTime 结合了原子钟和 GPS 时钟,使得误差相比 NTP 的 100ms 级别的误差减少到个位数毫秒的误差。
因此 TrueTime 返回的当前时间 now 会包含 earliest 和 latest 两个值,表示考虑误差下,当前时间最早和最晚可能是什么。
混合时钟(HLC)
例如,可以在每一秒重置逻辑时钟为0,然后每一次分配 TSO 都递增逻辑时钟。我们的 TSO 就是物理时间比如说是一秒,再加上逻辑时钟的值,而对准这 1s 是容易的。
To optimize performance of reads, CockroachDB implements hybrid-logical clocks (HLC) which are composed of a physical component (always close to local wall time) and a logical component (used to distinguish between events with the same physical component). This means that HLC time is always greater than or equal to the wall time. You can find more detail in the HLC paper.
在 CRDB 中,当节点发送消息给其他节点时,会发送基于自己的 HLC 生成的时间戳。当节点收到其他节点的消息时,When nodes receive requests, they inform their local HLC of the timestamp supplied with the event by the sender. This is useful in guaranteeing that all data read/written on a node is at a timestamp less than the next HLC time.
全序广播
逻辑时钟欠缺的部分(Timestamp ordering is not sufficient)
尽管通过 Lamport 时钟或者向量时钟可以得到一个符合因果一致性的全序关系,但这还不足以解决分布式系统中的常见问题。例如有两个用户正在竞争地创建具有相同用户名的账户,基于 Lamport 时间戳的方案可以使得具有更小的时间戳的请求成功。因为 timestamp 总是 total order 的,所以这个比较总是合法的。
但为了做这个判断,我们需要收集所有其他的节点,看看它们是否在并发地执行创建相同用户名的操作。试想,如果此时某个其他节点正在创建 username,但我们却不知道,那实际上就无法构建出最终的全序关系。
所以,我们无法立即返回这个请求是否能成功,特别地,如果出现了故障或者网络分区,则整个系统的可用性都受到了影响。
换句话说,知道所有操作的全序关系是不够的,还需要知道什么时候这些操作全部结束了。比如,如果有一个创建用户名的操作,那就需要确认没有其他 node 在之前有创建相同 username 的操作,才可以安全执行该操作。
容易发现,这甚至还不如一主多从复制的架构,毕竟后者能够容忍一些 Follower 的故障。为了解决“什么时候 total order 已经可以完成构建”的问题,引入了全序广播。
全序广播
那么回到一主多从的架构上。通过一主,可以很容易地确定一个全序关系,因为序列号或者时间戳的生成是单线程分配的。下面需要解决两个问题:
- 如何解决“一主”的吞吐量瓶颈
- 如何做 Fail Over
这样的问题被称为全序广播(total order boardcast) 或者原子广播(atomic broadcast)。有两个要求:
- Reliable delivery
消息不能被丢失:一个消息如果被传递到某个节点,那么一定能被传递到所有的节点。 - Totally ordered delivery
消息总是以相同的顺序传递给每个节点的。
这里的 Total order 即全序关系,是相对于偏序关系(partial order)的一个概念。全序要求在序列中的任何元素都能有确定的先后关系,而偏序则只要求序列中某些元素具有先后关系。整除关系是一个典型的偏序关系。
全序广播和因果一致
可以参考后面的 Causal 广播和 Total Order 广播的介绍。
全序广播和日志复制
全序广播和可串行化
全序广播可以被用来实现 serializable 的事务。如果每个 message 表示一个确定性的事务被执行,并且每个存储节点都按照相同的顺序处理这些消息,那么这个数据库的 Partition 和 Replica 彼此之间都是一致的。
全序广播和线性一致性
全序广播和线性一致性有什么关系呢?
全序广播是异步的,我们并不知道消息究竟何时能被送达。而线性一致一定能保证读取能看到最新的写入值。从这一点上,全序广播看起来更“弱”一点。
从一个更正式的观点来看,实现 linearizable read-write register 反而是一个更简单的问题。全序广播等价于实现共识,而 FLP 定理证明了异步的 Fail-stop 系统中,没有一个确定性的解法。但是 linearizable read-write register 却可以在相同的系统模型中实现,这里引用了论文 23 24 25,暂时还没看。但 Wait-Free Synchronization 这篇论文中支持,如果要在 register 中实现 CAS 操作的话,那么就等价于共识了。
其实下面可以看到,全序广播等于支持 CAS 的线性一致等于共识。这个在 Wait-Free Synchronization 中会有介绍。而诸如 Viewstamped Replicate、Paxos、Raft 之类的算法在实现共识时,都是通过决定值的 sequence 来决定的。也就是说实际上它们都是全序广播算法。特别地 Raft 等算法直接实现了全序广播,这个比像 Basic Paxos 那样的 one-value-at-a-time 的共识要更高效。
利用全序广播实现线性一致的存储
以先前的“创建相同用户名”为例,如果能够实现一个支持 CAS 操作的线性一致的 register,那么创建用户名就可以用这个 CAS 操作来实现。那如何实现这种线性一致的 CAS 呢?
- 向日志中添加一条 message,并尝试指定用户名。
- 不停地读取日志,直到刚才添加的 message 被 deliver 给自己。
这里还指出,如果我们不想等待 deliver,而是只要这个写入被放入队列中就返回,那么这就是类似多核 x86 处理器的 memory consistency model。而这既不是 linearizable 的,也不是 sequentially consistent 的。 - 然后检查受到的所有注册这个用户名的消息,如果第一条消息是来自于自己的,说明注册成功。可以 commit the username claim (perhaps by appending another message to the log),然后回复客户端。如果第一条消息不是来自于自己的,就 abort。
需要注意的是,以上我们可以得到一个线性一致的写入,但未必是线性一致的读取。实际上如果从一个从 log 异步更新的 store 中读取,则得到的数据可能是陈旧的。事实上这样的读取是顺序一致性(sequential consistency) 或者 timeline consistency,是一个比线性一致稍低的级别。
实现线性一致的读,有下面一些方法:
- 读取也要提交一条日志
这个类似于 Raft 上最基本的读操作,一般用于 Conf Change 过程中。 - 通过线性一致的方式获取最新的 message 的编号,并等待所有之前的 message 都 deliver 给自己
这个类似于 Raft 的 ReadIndex。 - 可以从同步复制的副本读取。
利用线性一致的存储实现全序广播
假设现在有一个线性一致的 register,并且它支持 CAS。那么可以令每个需要被全序广播发送的 message 都从这个 register 中用 CAS 分配一个全局唯一的自增 id,并将这个 id 附在 message 中。然后就可以向所有的节点发送 message,并在丢包的时候重传。接收方按照 id 依次 deliver 这些 message。
特别注意,不同于 Lamport 时间戳,这个 register 分配的 id 是连续的。例如带有 id=4 和 6 的 message 中间一定有个 id=5 的 message,所以它知道自己一定要等待。反之,它就知道自己已经收完了前面的消息了。这实际上就是全序广播和 timestamp ordering 的关键区别。
那么如何构建储一个支持 CAS 的线性一致 register 呢?如果不需要考虑各种 failure,那么只需要在某个 node 上用一个变量来维护就行了。但考虑到网络或者宕机等失效的问题,最终这些方案都会归结到共识算法。
实际上正如一直强调的那样,一个 linearizable 的 CAS 和 total order broadcase 都等价于共识算法。
全序广播扩展:各类广播及其实现
广播主要分为几个过程,从发送方发出消息的 broadcast 过程,消息在网络中传播的过程(可能会丢包乱序重复等),以及最后送达接受方的 deliver 过程。
广播根据 broadcast 和 deliver 的顺序可以分为下面几种类型,这些类型是依次增强的。从 FIFO 开始,对各种乱序的情况进行了规范。
- best effort 广播
- reliable 广播
引入重传 - FIFO 广播
如果 m1 和 m2 来自同一个 node,并且broadcast(m1)->broadcast(m2),这里箭头表示 happen before关系。那么 m1 也要在 m2 前面被 deliver。
通俗一点讲,就是从同一个节点 broadcast 出来的 message 的顺序和被 deliver 的顺序是一致的。但对于不同节点出来的 message,是无所谓顺序的。
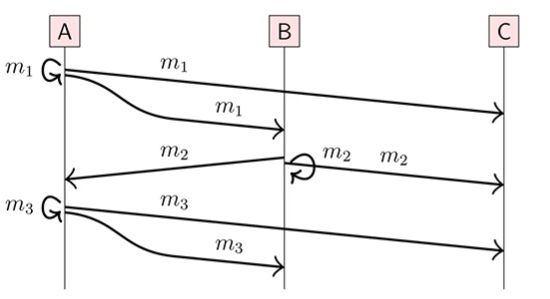
对于下面的图,到 C 节点的 deliver 顺序可以是213,123,132。
- Causal 广播
注意 Causal 表示因果的,不要和 casual 搞混。
如果broadcast(m1)->broadcast(m2),那么 m1 也要在 m2 前面被 deliver。
看起来,只是比 FIFO 广播少了“在同一个 node 上的条件”而已,实际差别是什么呢?其实在后面的文章中定义了 happen before,这里多了的就是 A 发消息,B 收消息这种跨 node 的 happen before 关系。照着 happen before 的三种情况,就容易理解了。
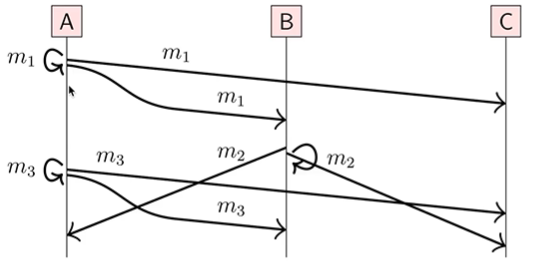
对于下面的图,如果broadcast(m1)->broadcast(m2)且broadcast(m1)->broadcast(m3),那么合法的 deliver 顺序是 123 和 132。
- Total Order 广播
如果在一个 node 上,m1 在 m2 前面被 deliver,那么在所有 node 上,m1 都在 m2 前面被 deliver。
既可以像下面的图一样,所有节点都按照 123 的顺序 deliver。这里需要看到来自 node A 的请求 m3,必须要 delay 到来自 node B 的请求 m2 被 deliver 之后才能 deliver,即使这个请求是自己发给自己的。
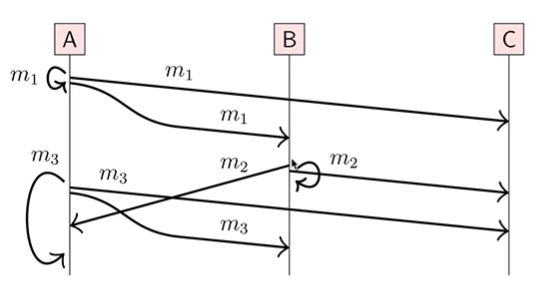
当然了,所有节点也可以按照 132 的顺序来 deliver,但这些顺序在所有节点上一定都是相同的。 - FIFO Total Order 广播
就是 FIFO 和 Total Order 的结合。
各类广播的实现
reliable
一个 naive 的想法是重传,同时处理重复包(例如可以通过编号的方式)。但如果在重传前传播的节点就宕掉了,那么 reliable 就无法保证。
一个简单的修复,就是每个节点在第一次收到消息之后,往其他节点转发一下消息。但这个行为会导致为了广播每一条消息,整个集群中总共发送 $O(n^2)$ 个消息。
Gossip 协议是对上述的一个优化。每个节点在第一次收到消息之后,会随机发送给 fanout 个节点(例如随机发给3个节点),有点像流行病毒传播一样。Gossip 协议能以很高的概率实现 reliable。
FIFO
对于每一个 node,维护下面几个变量:
- i
表示发送方 node 的编号 - seq
每个节点维护自己 broadcast 的信息的序号 - delivered[j]
是一个数组,表示对于 node j,我们总共 deliver 了几个序号 - buffer
用来存放尚未准备好 deliver 的信息
发送方发送信息 m,格式是 (i,seq,m)。在发送后,需要自增 seq。
接收方在接收来自 i 的信息后,先放到 buffer 中。接着在 buffer 中寻找 seq 等于 delivered[i] 的信息,如果存在,就 deliver,并且自增 delivered[i]。
这个方案实际上就是说接收方给每个发送方维护一个队列,通过这个队列保证自己收到来自 i 连续递增 seq 的信息。

Causal
发送方需要复制自己的 delivered 数组为 dep 数组,设置 dep[i] 为 seq。发送方发送 (i,deps,m)。在发送后,需要自增 seq。
接收方在收到某个消息 (i,deps,m) 之后,需要满足 deps<=delivered 条件之后,才能 deliver 这条信息。不过这个涉及到了比较两个数组,其规则就是之前提到的 vector clocks ordering。

Total Order
通常有两种方式:
- 借助 Leader
如果需要广播信息,则发送给 Leader。Leader 按照 FIFO 的方式广播信息。
这种方式需要解决 Leader 可能存在的单点问题。 - 借助于 Lamport timestamp
对每个消息加上 Lamport 时间戳,并且按照 Lamport 时间戳 deliver 消息。
如前所说,需要判断自己已经收到了所有 timestamp 小于 T 的所有消息。这需要使用 FIFO 连接,并且等到所有 node 上大于等于 T 的信息都被 deliver。
分布式快照
Chandy-Lamport 算法是用来实现分布式快照。
分布式快照需要解决什么问题呢?
- process 不能在同一个时刻记录下它们的状态,因为它们并没有一个一致的时钟。
- 我们实际需要每个 process 记录下本地状态,并彼此之间通过 channel 通信,从而得到一个 global system state。
- 在做分布式快照的同时,不能破坏系统的运行。例如不能强制系统暂停。
这里作者打了一个比方,好像有一队的摄影师去拍一个全景的、动态的风景。但这个风景不能被一次性拍摄完,所以得拍出很多张照片,再最后拼接起来。作者强调拼接得到的照片应该是 meaningful 的。
在分布式领域,很多问题都可以被形式化为设计一种算法,判定系统 D 中某个性质 y 是否成立。例如 Deadlock detection,或者 Termination detection。 也就是说系统 D 处于某个全局状态 S,并且后续可以到达的全局状态的集合是 S’。如果 y(S) 是 true/false,则 y(S’) 是 true/false,那么 y 是一个 stable property。
。
下面介绍整个系统的抽象,process 之间由 channel 连接。Channel 是 error-free 的,并且会按照 sent 的顺序有序地 deliver 消息。Channel 中消息传递的延迟是随机但是有限的。process p 中的一个 event e 是一个原子操作,它要么修改 p 的状态,要么向一个 Channel 发送一个消息,从而改变这个 Channel 的状态,或者从一个 Channel 接收消息。
因此 e 可以被 <p, s, s', M, c> 定义。其中 s 是 e 之前 p 的状态,s’ 是 e 之后 p 的状态,c 是被修改的 Channel。next(S, e) 表示系统在发生 e 之后的状态。
下面定义了一个叫 single token conversation 的系统。每个 process 有两个 state,s0 表示自己不持有 token,s1 表示自己持有 token。这四个状态分别起名为 in-p、in-c、in-q、in-c’。这个定义也很直观。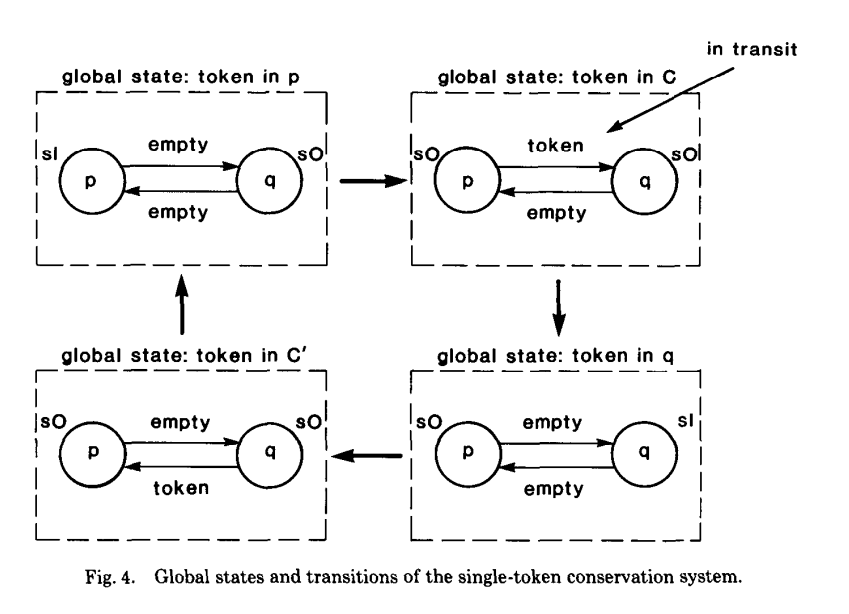
一个 system computation 和 global state 之间的转换相关。比如 (p send token,q recv token) 就是一个 computation,但 (p send token,q recv token) 就不是一个 computation。
算法
每个 process 记录自己的状态,每个 channel 由事件发生的两个 process 记录各自的状态。我们并不指望这些状态都在同时被记录下来,但它们得是 meaningful 的。这个 Snapshot 算法必须和系统本身的计算同时进行,但不能改变本来的这些计算。
我们需要避免下面这样的情况:一开始处于 in-p 状态,此时 Snapshot 算法启动,记录下了 p 持有 token 的状态。然后 p 发送了 token,所以进入了 in-c 状态。所以此时 c 的状态显示持有 token,而 c’ 和 q 的状态显示不持有 token。可以看出,最后得到的 global state 显示 p 和 c 中都持有 token,这显然不是 meaningful 的状态。
令 n 为在记录 p 的状态前,从 c 发送的消息的数量。令 n’ 在记录 c 的状态前,从 c 发送的消息的数量。上面的 demo 说明了,如果 n 小于 n’,记录得到的 global state 可能是不一致的。
考虑另一个场景,假设此时记录了 c 为状态是 in-p,然后系统进入了 in-c,然后 c’、p、q 的状态都记录为 in-c。此时最终得到的 Snapshot 显示系统中没有 token。这说明了,如果 n 大于 n’,记录得到的 global state 可能是不一致的。
同理,设 m 是在记录 q 的状态前,从 c 接收的消息的数量。设 m’ 是在记录 c 的状态前,从 c 接收的消息的数量。
并且,c 发送的消息的数量,一定小于等于 c 接收的消息的数量。其实可以连同上面两个结论,得到下面三个等式
1 | n = n' |
即
1 | n >= m |
那么,channel c 被记录的状态:
- 一定不包含 sender 记录状态之后的发送事件
- 一定不包含 receiver 记录状态之后的接收事件
特别地,如果 n’ 等于 m’,那么记录下来的 c 一定是一个空的序列。如果 n’ 大于 m’,那么记录下来的 c 一定是 (m'+1) 到 n 这些消息,也就是发出去的,但是还没有被对端接受的消息。
通过上面的推理,可以得到一个简单的算法。process p 会在向 c 发送完第 n 个消息之后,发送一个特殊的消息,称为 marker。这个 marker 对 underlying computation 没有额外影响,但是在往 c 发送后续的消息之前,需要先发送这个 marker。c 的状态是,在 q 记录完自己的状态之后,并且收到 marker 之前收到的消息。为了确保满足 n >= m,如果 q 在收到 marker 之后还没有记录自己的状态,那就需要在收后续的消息之前,先记录自己的状态。
算法如下图所示:
- p 部分
对于所有从 p 发出消息的 channel c,先记录自己状态,再发送 marker,然后才能发送后续的消息。 - q 部分
如果从某个 channel c 收到 marker 消息,那么如果 q 还没有记录自己的状态,就记录,并且记录 c 的状态为空 sequence。
如果已经记录过了,就记录 c 的状态为从自己记录状态开始,到收到 marker 前的所有消息。
比如说,假设 p 发起了 global snapshot 过程,并且 p 已经做过了 local snapshot,那么当它收到 q 的 [a, b] 消息的时候,需要记录这些消息。直到 p 收到了 q 的 marker 之后,后续收到的 q 的消息,才可以不记录。

分布式共识
本章将原先分布式一致性和分布式共识协议中一些理论性较强的部分单独讲解。
分布式共识的特性
具体地讲,一个正确的分布式共识算法应当满足以下特性:
- agreement
决议需要得到所有节点的认同,通常是首先批准一个多数票的决议,然后进行同步。 - integrity
没有节点能投两票。 - validity
决议的值需要满足合法性要求。比如不会产生一些平凡的决议:例如无论是什么输入,都投票 null。 - termination(liveness)
决议过程能够在有限步内结束,并产生结果。
以上特性还可以总结成两点,safety 和 liveness:
- safety 要求系统不会产生一个错误的值
以分布式事务为例,safety 要求一个进程提交则全体进程提交,一个进程回滚则全部进程回滚 - liveness 要求系统不至于陷入阻塞。
以分布式事务为例,liveness 要求如果没有故障,并且可提交则立即提交;如果有故障则立即回滚。
而 2PC 就存在 liveness 的问题。当协调者宕机后,termination 不满足。
其实在写 TLA+ 验证一些系统的实现时,很多 Invariant 就是围绕 safety 和 liveness 来写的。
分布式共识和分布式事务
共识协议能够让一个集群的行为如同一个单机节点一样,即使其中有一小部分的节点宕机或分区。
分布式事务面临解决原子提交(atomic commit)的问题。如果想维护事务的 ACID 中的原子性,就需要让所有节点就数据是否提交达成一致。而这也可以被理解为一种共识。2PC 就是实现这种共识的一种办法,虽然它可能不是很好。
区别
分布式事务涉及的是对多个值修改的 ACID 性质。分布式共识协议是为了管理一个值的多个 replica。知乎上有一些讨论,我们可以认为 2PC 针对多个 Partition,而共识算法针对于多个 Replication。
再从可用性上考虑,诸如 Raft 的分布式共识协议是为了维护复制状态机和全序广播,从而实现线性一致。所以有两点 2PC 不具备的:
- 选主策略用来改善高可用性
2PC 的 Leader,也就是协调者在宕机之后集群会整体阻塞。 - Quorum
2PC 需要全体同意才能提交。
从 CAP 理论上来讲:
- 2PC 是 CA 的,它要求所有节点保持全体一致。
- 诸如 Paxos 的 Quorum 类算法是CP的,它仅要求实现多数一致。
- RWN 是 AP 的,因此它实现的是可调一致性而不是强一致性。
那么,共识协议有什么缺点呢?我理解 2PC 并不需要一个 Total order 来定序。
FLP定理
拜占庭将军问题
拜占庭将军问题指在一个有 N 个节点的集群内部,有 F 个节点可能发生任意错误的情况下,如果 N <= 3F ,一个正确的共识不可能达成。这里的任意错误包括节点前后的行为不一致,例如在投票时投给两个不同的节点。
诸如 Paxos 之类的算法只能对节点宕机进行容错,而不能对节点的拜占庭故障进行容错。这类基于复制状态机实现的协议,需要N >= 2F + 1才能确保共识的达成。
实用拜占庭容错算法(Pratical Byzantine Fault Tolerance, PBFT)是一种多项式复杂度的状态机复制算法。
CAP 定理
CAP 理论认为一致性(consistency)、可用性(availability)和分区容错性(partition tolerance)是不可能同时被满足的。
CAP 论文中讨论了四种一致性:
- Trivial services
这种服务不需要在节点间协调,因此不是论文的讨论对象 - Weakly consistent services
- Simple services
这是论文关注的主要对象。这个一致性主要包含两点:- sequential
- atomic
- Complicated services
这里的证明大概可以理解为,一致性要求当某个节点返回给客户端某个值之后,所有节点不能返回给客户端更旧的值。但如果发生了分区故障,写入节点就无法将新的数据发送给所有节点了。而可用性又要求任何一个节点不能拒绝客户端的请求,这就逼迫被分区的节点必须要返回一个更旧的值。
如果将这里的Consistency 替换为 Consensus(实际上两者说的不是一个东西),那么根据 FLP 定理,异步系统上无法保证 CA,所以只能选择 CP 和 AP。比如 Paxos、Raft 等系统实际上都是有 Liveness 问题的。这很能理解,例如 Raft 可能无限在选主过程中徘徊。
但在工程上,CAP 是可以被优化的,例如:
- 可以引入一些同步机制,当一个节点与其他节点分区达到超时时间后,就会去声明自己宕掉了。
- 使用像 Redis Sentinel 一样的机制,使用另外一套班子来检测集群的状态。
Leader
复制状态机
复制状态机(Replicated State Machine, RSM)由 Lamport 提出,源自 Paxos 算法。复制状态机通过同步日志,使得多个节点从相同的初始状态开始,按顺序执行相同的命令,转移到相同的状态。容易看出,复制状态机的关键点是如何让每个状态机就提交顺序达成一致。因此,分布式共识协议常被用作在复制状态机的上下文中。
复制状态机中向所有节点同步的内容是操作本身,我们可以理解为同步的是某个值的增量。与复制状态机相对应的是在 ZAB 等协议中常出现的 primary backup system,它向所有节点同步的是操作的结果,我们可以认为同步的是值本身。容易看出 RSM 的设计使得回滚操作变得简单,仅仅删除掉后面的日志即可,但不好的地方在于 RSM 往往需要比 PBS 系统较多的日志条目,因为 PB S 可以只保存对状态机有修改的操作。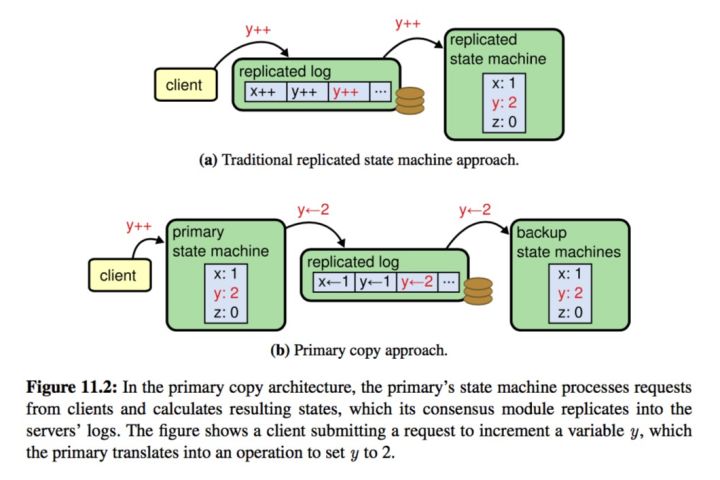
基于 RSM 的日志复制形式是 State-machine replication,能够实现 FT。
SMR 的性能
通常的 SMR 的实现是串行的,即每个 SMR 副本以单线程的形式处理Propose-Append-Broadcast-Apply的过程。只有当客户 A 的请求 Apply 之后,才能继续处理客户 B 的 Propose。事实上,SMR 的一个实现细节就是为所有的输入选择一个特定的顺序。
尽管现实中的输入往往是因果也就是偏序的,但 SMR 要求一个全序(total order)的输入。这样每一个非故障的副本才能在同样的状态通过同样的输入到达同样的结果。
分布式共识算法被用来解决 SMR 中存在的问题,例如如何选主,如何处理网络分区等,常见的分布式共识算法包括 Paxos 和 Raft 等。这里的共识(Consensus)指的是由一系列独立的实体为一个值进行投票。
Pipeline 是对串行方式 SMR 的一个优化,即使用一个线程接收请求,一个线程处理请求,一个线程响应客户端。
SMR 的容错和副本数量之间的关系
根据 Wikipedia,有下面几种情况:
- 一般来说一个支持 F 个独立随机的故障的系统需要
2F+1个 replica
这里发生故障后,系统可能继续处理,并且产生一些伪造的或者错误的消息。
不过我觉得这里应该针对的是 Crash(Fail)-Recovery 模型,也就是节点在 Crash 之后有可能恢复。 - 对于 Fail-Stop 情况,只需要
F+1个 replica。
这里的故障要求系统保证不产生任何输出。
目前没有系统做到这一点。 - 对于拜占庭故障,即某个节点向不同方向发送不同值的情况下,根据消息是否加密验证需要
2F+1和3F+1个 replica。
Reference
- http://yang.observer/2020/07/11/time-ntp/
介绍计算机中的时钟 - Time, Clocks, and the Ordering of Events in a Distributed System
Lamport的有关分布式时钟的论文 - https://zhuanlan.zhihu.com/p/56886156
对向量时钟的一个讲解 - https://writings.sh/post/logical-clocks
同样是对逻辑时钟的讲解,我这边摘录了他的几幅图 - https://www.raychase.net/5768
用了其中的图和某个case - http://gaocegege.com/Blog/%E9%9A%8F%E7%AC%94/consistency
论述了Linearizability和Serializability的区别。即“Linearizability 要求操作生效的顺序等于实际的实时操作排序。Serializability 允许操作被重新排序,只要在每个节点上观察到的顺序保持一致。作为用户, 能区分两者的唯一方法是,观察系统的所有输入和时间. 从客户端与节点交互的角度来看,两者是等价的” - Perspectives on the CAP Theorem
CAP 定理的论文 - Impossibility of distributed consensus with one faulty process
FLP 定理的论文 - https://www.zhihu.com/question/275845393/answer/386816571
- https://learn.microsoft.com/zh-cn/azure/cosmos-db/consistency-levels
介绍了一些一致性级别。 - https://blog.csdn.net/chao2016/article/details/81149674#%E5%8E%9F%E5%AD%90%E4%B8%80%E8%87%B4%E6%80%A7atomic-consistency
- https://www.microsoft.com/en-us/research/uploads/prod/2016/12/Determining-Global-States-of-a-Distributed-System.pdf
Lamport Snapshot

